题目内容
定义函数F(x,y)=(1+x)y,x,y∈(0,+∞).
(1)令函数f(x)=F[1,log2(x3-3x)]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
(2)令函数g(x)=F[1,log2(x3+ax2+bx+1)]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
(3)当x,y∈N*,且x<y时,证明F(x,y)>F(y,x).
(1)令函数f(x)=F[1,log2(x3-3x)]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
(2)令函数g(x)=F[1,log2(x3+ax2+bx+1)]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
(3)当x,y∈N*,且x<y时,证明F(x,y)>F(y,x).
分析:(1)由函数F(x,y)的定义可求得f(x),根据垂直关系可得切线斜率即f′(x)值,从而可求得切点坐标,求出切线方程.
(2)曲线C2在x0(x0∈(1,4))处存在斜率为-8的切线,即g′(x0)=-8有解,由已知消去b转化为关于a,x的不等式即可解得.
(3)F(x,y)>F(y,x)?(1+x)y>(1+y)x?yln(1+x)>xln(1+y)?
>
,构造函数h(x)=
,利用导数判断h(x)单调递减即可.
(2)曲线C2在x0(x0∈(1,4))处存在斜率为-8的切线,即g′(x0)=-8有解,由已知消去b转化为关于a,x的不等式即可解得.
(3)F(x,y)>F(y,x)?(1+x)y>(1+y)x?yln(1+x)>xln(1+y)?
| ln(1+x) |
| x |
| ln(1+y) |
| y |
| ln(1+x) |
| x |
解答:解:(1)f(x)=F[1,log2(x3-3x)]=(1+1)log2(x3-3x)=x3-3x,
由log2(x3-3x)>0,得x3-3x>1.又f′(x)=3x2-3=
,由f′(x)=0,得x=±
,
∵x3-3x>1,∴x=-
.又f(-
)=
,∴切点为(-
,
).
∴存在与直线4x+15y-3=0垂直的切线,其方程为y-
=
(x+
),即15x-4y+27=0.
(2)g(x)=[1,log2(x3+ax2+bx+1)]=x3+ax2+bx+1.
由log2(x3+ax2+bx+1)>0,得x3+ax2+bx>0,
由g′(x)=3x2+2ax+b=-8,得b=-3x2-2ax-8,
x3+ax2+bx=x3+ax2+x(-3x2-2ax-8)=-2x3-ax2-8x>0在(1,4)上有解,
∴2x2+ax+8<0在(1,4)上有解,即a<-2x-
在(1,4)上有解,∴a<(-2x-
)max(1<x<4),
而-2x-
=-(2x+
)≤-2
=-8,当且仅当x=2时取等号,∴a<-8.
故实数a的取值范围为(-∞,-8).
证明:(3)F(x,y)>F(y,x)?(1+x)y>(1+y)x?yln(1+x)>xln(1+y)?
>
,
令h(x)=
,则h′(x)=
,当x≥2时,
<1<ln(1+x),
∴h′(x)<0,h(x)单调递减.
∴当2≤x<y时,h(x)>h(y),又当x=1且y=2时,h(1)=ln2>
ln3=h(2).
故当x,y∈N*,且x<y时,h(x)>h(y),即F(x,y)>F(y,x).
由log2(x3-3x)>0,得x3-3x>1.又f′(x)=3x2-3=
| 15 |
| 4 |
| 3 |
| 2 |
∵x3-3x>1,∴x=-
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |
∴存在与直线4x+15y-3=0垂直的切线,其方程为y-
| 9 |
| 8 |
| 15 |
| 4 |
| 3 |
| 2 |
(2)g(x)=[1,log2(x3+ax2+bx+1)]=x3+ax2+bx+1.
由log2(x3+ax2+bx+1)>0,得x3+ax2+bx>0,
由g′(x)=3x2+2ax+b=-8,得b=-3x2-2ax-8,
x3+ax2+bx=x3+ax2+x(-3x2-2ax-8)=-2x3-ax2-8x>0在(1,4)上有解,
∴2x2+ax+8<0在(1,4)上有解,即a<-2x-
| 8 |
| x |
| 8 |
| x |
而-2x-
| 8 |
| x |
| 8 |
| x |
2x•
|
故实数a的取值范围为(-∞,-8).
证明:(3)F(x,y)>F(y,x)?(1+x)y>(1+y)x?yln(1+x)>xln(1+y)?
| ln(1+x) |
| x |
| ln(1+y) |
| y |
令h(x)=
| ln(1+x) |
| x |
| ||
| x2 |
| x |
| 1+x |
∴h′(x)<0,h(x)单调递减.
∴当2≤x<y时,h(x)>h(y),又当x=1且y=2时,h(1)=ln2>
| 1 |
| 2 |
故当x,y∈N*,且x<y时,h(x)>h(y),即F(x,y)>F(y,x).
点评:本题考查了导数的几何意义、利用导数研究函数的单调性,运用所学知识解决新问题的能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
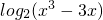 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;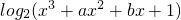 ]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x0(x0∈(1,4))处有斜率为-8的切线,求实数a的取值范围;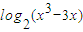 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程; ]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;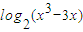 ]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程;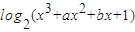 ]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;
]的图象为曲线C2,若存在实数b使得曲线C2在x(x∈(1,4))处有斜率为-8的切线,求实数a的取值范围;