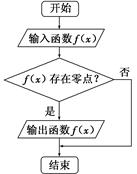
题目内容
形如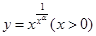 的函数称为“幂指型函数”,它的求导过程可概括成:取对数——两边对
的函数称为“幂指型函数”,它的求导过程可概括成:取对数——两边对 求导——代入还原;例如:
求导——代入还原;例如: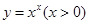 ,取对数
,取对数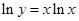 ,对
,对 求导
求导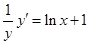 ,代入还原
,代入还原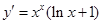 ;给出下列命题:
;给出下列命题:
①当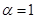 时,函数
时,函数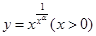 的导函数是
的导函数是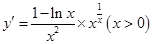 ;②当
;②当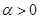 时,函数
时,函数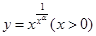 在
在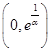 上单增,在
上单增,在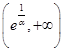 上单减;③当
上单减;③当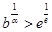 时,方程
时,方程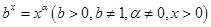 有根;④当
有根;④当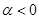 时,若方程
时,若方程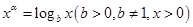 有两根,则
有两根,则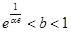 ;
;
其中正确的命题是
①②④
解析试题分析:对①,当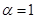 时,函数
时,函数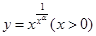 即为
即为 ,两边取对数得
,两边取对数得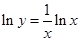 ,两边求导得
,两边求导得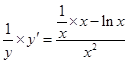 ,将
,将 代入即得
代入即得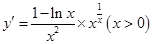 ;正确.
;正确.
对②,当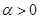 时,函数
时,函数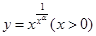 两边取对数得
两边取对数得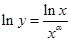 ,两边取对数得
,两边取对数得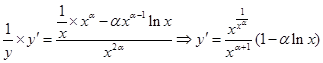 .由
.由 得
得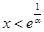 ,所以
,所以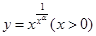 在
在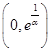 上单增,在
上单增,在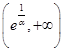 上单减,正确;
上单减,正确;
对③,由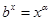 得
得 .令
.令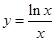 ,则
,则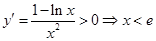 ,所以
,所以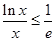 .所以当
.所以当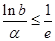 时,
时,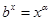 有解.由
有解.由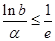 得
得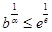 ,故③错;
,故③错;
对④,由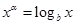 得
得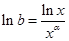 .令
.令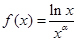 ,则
,则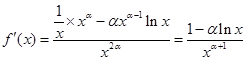 .因为
.因为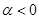 ,所以
,所以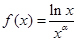 在
在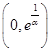 上单减,在
上单减,在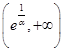 上单增,
上单增,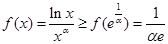 .所以当
.所以当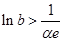 时,若方程
时,若方程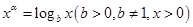 有两根.由
有两根.由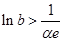 得,
得,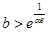 .又结合图象易得,当
.又结合图象易得,当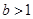 时方程
时方程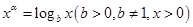 只有一个根,所以
只有一个根,所以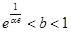 .
.
考点:新定义及导数的应用.

练习册系列答案
相关题目
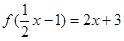 ,且
,且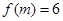 ,则
,则 等于 .
等于 .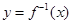 是函数
是函数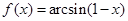 的反函数,则
的反函数,则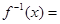 .
.
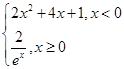 ,则f(x)的“友好点对”有________个.
,则f(x)的“友好点对”有________个.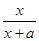 在(-2,+∞)上为增函数,则a的取值范围是________.
在(-2,+∞)上为增函数,则a的取值范围是________.