题目内容
18.考察正三角形三边中点及3个顶点,从中任意选4个点,则这4个点顺次连成平行四边形的概率等于$\frac{1}{5}$.分析 从等边三角形的三个顶点及三边中点中随机的选择4个,共有${C}_{6}^{4}$=15种选法,其中4个点构成平行四边形的选法有3个,由此能求出4个点构成平行四边形的概率.
解答 解:从等边三角形的三个顶点及三边中点中随机的选择4个,共有${C}_{6}^{4}$=15种选法,
其中4个点构成平行四边形的选法有3个,
∴4个点构成平行四边形的概率P=$\frac{3}{15}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查古典概型及其概率计算公式的应用,是基础题.确定基本事件的个数是关键.

练习册系列答案
相关题目
6.已知p:x≤1,q:x2-x>0,则p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
13.若复数(2+ai)2(a∈R)是实数(i是虚数单位),则实数a的值为( )
| A. | -2 | B. | ±2 | C. | 0 | D. | 2 |
3.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )


| A. | 8π | B. | 16π | C. | 32π | D. | 64π |
10.已知抛物线C:y2=8x焦点为F,点P是C上一点,若△POF的面积为2,则|PF|=( )
| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
 与向量
与向量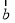 的夹角为钝角,
的夹角为钝角,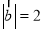 ,且当
,且当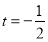 时,
时, 取最小值
取最小值 .向量
.向量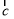 满足
满足 ,则当
,则当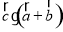 取最大值时,
取最大值时,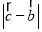 等于( )
等于( ) B.
B.
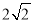 D.
D.
 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).