题目内容
8.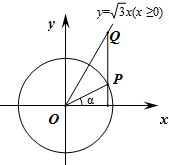 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=√3x(x≥0)交于点Q,其中α∈(-π2,π2).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=√3x(x≥0)交于点Q,其中α∈(-π2,π2).(Ⅰ)若sinα=13,求cos∠POQ;
(Ⅱ)求→OP•→OQ的最大值.
分析 (Ⅰ)易得∠POQ=π3−α,由三角函数的和差公式即可计算;
(Ⅱ)用坐标表示出点P、Q,利用辅助角公式将式子进行化简,结合三角函数的图象和性质即可求出数量积的最大值.
解答 解:(Ⅰ)∵sinα=13,α∈(−π2,π2),
∴cosα=2√23,α<π3.
∵∠MOQ=π3,且α<π3,
∴∠POQ=π3−α,
∴cos∠POQ=cos(π3−α)=cosπ3cosα+sinπ3sinα=2√2+√36;
(Ⅱ)∵P(cosα,sinα),
∴Q(cosα,√3cosα)
∴→OP•→OQ=cos2α+√3sinα•cosα=12cos2α+√32sin2α+12=sin(2α+π6)+12,
∵α∈(−π2,π2),
∴−5π6<2α+π6<7π6,
所以,当2α+π6=π2,即α=π6时,→OP•→OQ取最大值32.
点评 本题主要考查三角函数的定义以及两角和差公式的应用,以及向量数量积的计算,根据三角函数的定义求出点P、Q的坐标是解决本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.司机甲、乙加油习惯不同,甲每次加定量的油,乙每次加固定钱数的油,恰有两次甲、乙同时加同单价的油,但这两次的油价不同,则从这两次加油的均价角度分析( )
| A. | 甲合适 | B. | 乙合适 | ||
| C. | 油价先高后低甲合适 | D. | 油价先低后高甲合适 |
 如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为
如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为 如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为
如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为