题目内容
解答题
已知双曲线x2-![]() =1,问过点P(1,1)能否作一条直线l与双曲线交于A、B两点,且点P恰是弦AB的中点?
=1,问过点P(1,1)能否作一条直线l与双曲线交于A、B两点,且点P恰是弦AB的中点?
答案:
解析:
解析:
|
假设存在这样的直线l,由双曲线对称性易知,l斜率必存在. 设A(x1,y1),B(x2,y2),(x1≠x2)、 ∵P(1,1)是AB中点,∴x1+x2=2,y1+y2=2, ∴k= 但是由 ∴直线2x-y-1=0与双曲线无公共点,故直线l不存在. |

练习册系列答案
相关题目
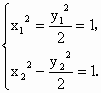 相减得
相减得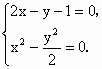 消去y后得到2x2-4+3=0,Δ<0.
消去y后得到2x2-4+3=0,Δ<0. -
- =1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足
=1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足 、
、 、
、 成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.
成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.
 ·
· =
= ·
· ;
;