题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:设双曲线C的渐近线方程为y=kx,即kx-y=0 ∵该直线与圆 ∴双曲线C的两条渐近线方程为 故设双曲线C的方程为 ∴ |
(2) |
解:若Q在双曲线的右支上,则延长QF2到T,使|QT|=|OF1| 若Q在双曲线的左支上,则在QF2上取一点T,使|QT|=|QF1| 根据双曲线的定义|TF2|=2,所以点T在以F2 由于点N是线段F1T的中点,设N(x,y),T( 则 代入①并整理得点N的轨迹方程为 |
(3) |
解:由 令 直线与双曲线左支交于两点,等价于方程 因此 又AB中点为 ∴直线L的方程为 令x=0,得 ∵ ∴故b的取值范围是 |

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
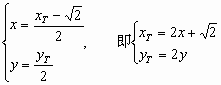
 ……………………………………………10分
……………………………………………10分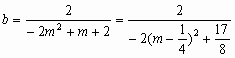
 和直线l交于点Q,求点Q的轨迹方程,并指出该轨迹的名称和焦点坐标.
和直线l交于点Q,求点Q的轨迹方程,并指出该轨迹的名称和焦点坐标.