题目内容
已知双曲线C: -
- =1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足
=1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足 、
、 、
、 成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.
成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线l,垂足为P.

(Ⅰ)求证: ·
· =
= ·
· ;
;
(Ⅱ)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.
答案:
解析:
解析:
|
解:(Ⅰ)法一,l:y=-
∵ ∴A( ∴ ∴ 法二:同上得P( ∴PA⊥x轴. ∴ (Ⅱ) 即(b2- ∵x1·x2= ∴b4>a4,即b2>a2,c2-a2>a2. ∴e2>2.即e> |

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
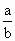 (x-c),
(x-c),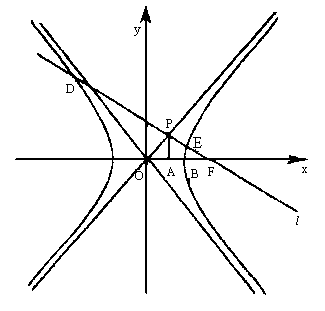
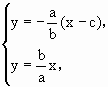 解得P(
解得P(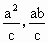 ).
).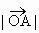 、
、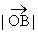 、
、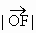 成等比数列,
成等比数列,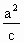 ,0).∴
,0).∴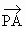 =(0,-
=(0,-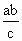 ).
).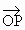 =(
=(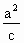 ,
, =(-
=(-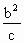 ,
,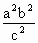 ,
, ·
·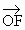 =0.
=0.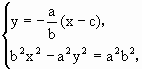 ∴b2x2-
∴b2x2-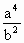 (x-c)2=a2b2.
(x-c)2=a2b2.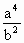 )x2+2
)x2+2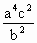 +a2b2)=0,
+a2b2)=0,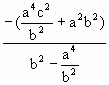 <0,
<0,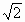 .
.