题目内容
(本小题满分15分)已知二次函数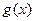 对
对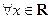 都满足
都满足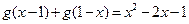 且
且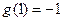 ,设函数
,设函数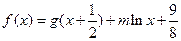
(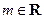 ,
,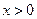 ).
).
(1)求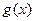 的表达式;
的表达式;
(2)若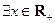 ,使
,使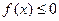
 成立,求实数
成立,求实数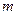 的取值范围;
的取值范围;
(3)设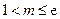 ,
,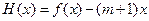 ,求证:对于
,求证:对于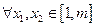 ,恒有
,恒有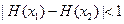 .
.
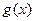 对
对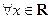 都满足
都满足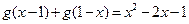 且
且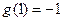 ,设函数
,设函数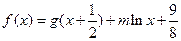
(
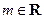 ,
,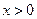 ).
).(1)求
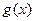 的表达式;
的表达式;(2)若
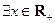 ,使
,使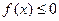
 成立,求实数
成立,求实数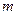 的取值范围;
的取值范围;(3)设
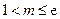 ,
,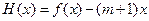 ,求证:对于
,求证:对于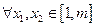 ,恒有
,恒有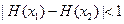 .
. 解:(1)设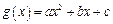 ,于是
,于是
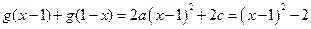 ,所以
,所以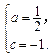
又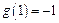 ,则
,则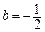 .所以
.所以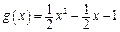 .
.
(2)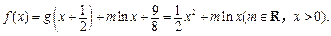
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,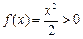 对
对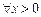 ,
,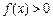 恒成立;
恒成立;
当m<0时,由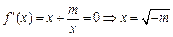 ,
,
列表:
这时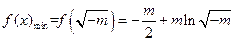 ,
,
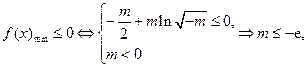
综上,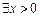 使
使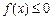 成立,实数m的取值范围
成立,实数m的取值范围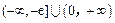 .
.
(3)由题知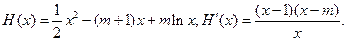 因为对
因为对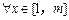 ,
,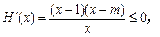 所以
所以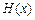 在
在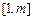 内单调递减.
内单调递减.
于是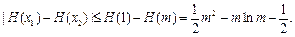
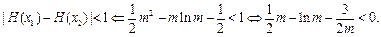
记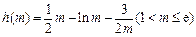 ,则
,则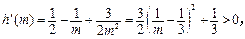
所以函数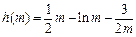 在
在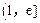 是单调增函数,
是单调增函数,
所以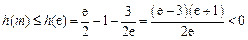 ,故命题成立.
,故命题成立.
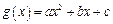 ,于是
,于是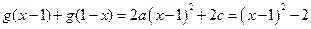 ,所以
,所以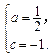
又
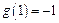 ,则
,则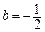 .所以
.所以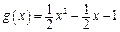 .
. (2)
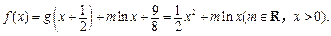
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,
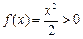 对
对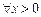 ,
,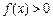 恒成立;
恒成立; 当m<0时,由
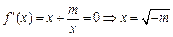 ,
,列表:
| x | 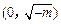 | 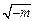 | 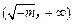 |
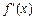 | - | 0 | + |
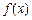 | 递减 | 极小值 | 递增 |
这时
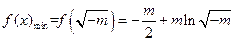 ,
,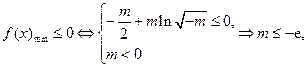
综上,
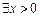 使
使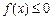 成立,实数m的取值范围
成立,实数m的取值范围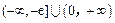 .
.(3)由题知
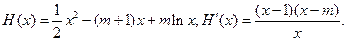 因为对
因为对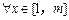 ,
,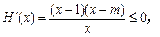 所以
所以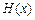 在
在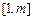 内单调递减.
内单调递减.于是
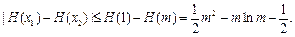
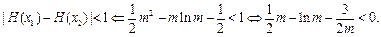
记
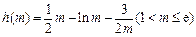 ,则
,则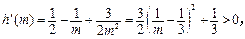
所以函数
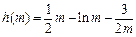 在
在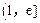 是单调增函数,
是单调增函数, 所以
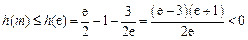 ,故命题成立.
,故命题成立. 略

练习册系列答案
相关题目
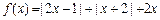 (
(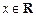 ),
),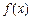 的最小值;
的最小值;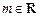 ,命题p:关于x的不等式
,命题p:关于x的不等式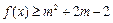 对任意
对任意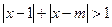 对任意
对任意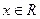 恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围.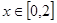 时,函数
时,函数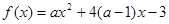 在
在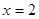 时取得最大值,则a的取值范围是
时取得最大值,则a的取值范围是 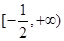
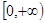
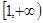
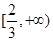
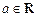 ,
,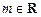 ,函数
,函数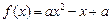 。若
。若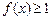 对
对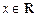 都成立,求
都成立,求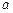 的取值范围。
的取值范围。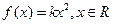 的图像上的任意一点都在函数
的图像上的任意一点都在函数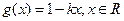 的下方,则实数
的下方,则实数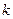 的取值范围是___________
的取值范围是___________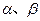 是方程
是方程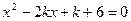 的两个实根,则
的两个实根,则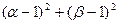 的最小值是________
的最小值是________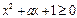 对一切
对一切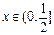 成立,则
成立,则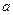 的最小值为 ( )
的最小值为 ( )


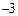
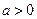 ,函数
,函数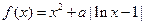 .
.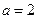 时,求函数
时,求函数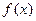 的单调增区间;
的单调增区间;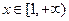 时,不等式
时,不等式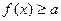 恒成立,实数
恒成立,实数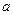 的取值范围
的取值范围