题目内容
【题目】在二项式![]() 的展开式中,
的展开式中,
(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(最后结果用算式表达,不用计算出数值)
(2)若展开式前三项的二项式系数的和等于79,求展开式中系数最大的项.(最后结果用算式表达,不用计算出数值)
【答案】(1) 当![]() 时,最大项系数为
时,最大项系数为![]() 和
和![]() ;当
;当![]() 时最大项系数为
时最大项系数为![]() .(2)
.(2) ![]() .
.
【解析】
(1)由![]() 成等差数列可求出
成等差数列可求出![]() 或
或![]() ,进而可求出展开式中二项式系数最大的项的系数;
,进而可求出展开式中二项式系数最大的项的系数;
(2)由![]() 可求出
可求出![]() ,令
,令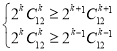 可求出
可求出![]() ,从而可求其系数.
,从而可求其系数.
解:展开式中第![]() 项为
项为![]() .
.
(1) 则第5项、第6项与第7项的二项式系数为![]() 成等差数列,则
成等差数列,则![]() ,
,
即![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,二项式系数最大项为
时,二项式系数最大项为![]() ,此时系数为
,此时系数为![]() 和
和![]() .
.
当![]() 时,二项式系数最大项为
时,二项式系数最大项为![]() ,此时系数为
,此时系数为![]() .
.
(2) 前三项的二项式系数为![]() ,其和为79.即
,其和为79.即![]() ,即
,即
![]() ,整理得,
,整理得,![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
设展开式中第![]() 项系数最大,即
项系数最大,即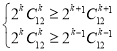 ,解得,
,解得,![]() ,
,
因为![]() ,所以
,所以![]() ,即展开式中第9项系数最大,系数为
,即展开式中第9项系数最大,系数为![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目