题目内容
设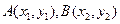 为抛物线
为抛物线
 上位于
上位于 轴两侧的两点。(1)若
轴两侧的两点。(1)若 ,证明直线
,证明直线 恒过一个定点;(2)若
恒过一个定点;(2)若 ,
,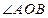
 为钝角,求直线
为钝角,求直线 在
在 轴上截距的取值范围。
轴上截距的取值范围。
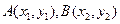 为抛物线
为抛物线
 上位于
上位于 轴两侧的两点。(1)若
轴两侧的两点。(1)若 ,证明直线
,证明直线 恒过一个定点;(2)若
恒过一个定点;(2)若 ,
,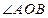
 为钝角,求直线
为钝角,求直线 在
在 轴上截距的取值范围。
轴上截距的取值范围。(1)证明略(2)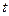 的取值范围是
的取值范围是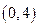
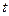 的取值范围是
的取值范围是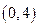
(1)设直线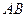 在
在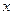 轴上的截距为
轴上的截距为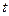 ,直线
,直线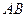 的方程为
的方程为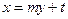 ,代入
,代入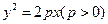 ,得
,得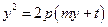 ,即
,即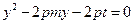 ,于是
,于是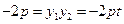 ,所以
,所以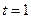 ,即直线
,即直线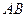 恒过定点
恒过定点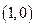 ,(2)∵
,(2)∵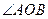 (
(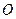 为坐标原点)为钝角,所以
为坐标原点)为钝角,所以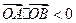 ,即
,即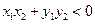 ,∵
,∵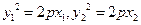 ,∴
,∴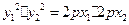 ,于是
,于是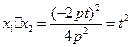 ,
,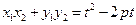 =
=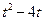
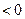 ,解得
,解得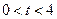 ,即
,即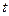 的取值范围是
的取值范围是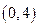 。
。
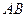 在
在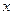 轴上的截距为
轴上的截距为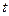 ,直线
,直线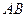 的方程为
的方程为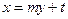 ,代入
,代入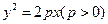 ,得
,得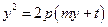 ,即
,即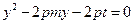 ,于是
,于是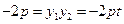 ,所以
,所以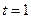 ,即直线
,即直线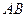 恒过定点
恒过定点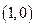 ,(2)∵
,(2)∵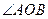 (
(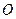 为坐标原点)为钝角,所以
为坐标原点)为钝角,所以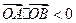 ,即
,即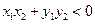 ,∵
,∵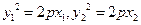 ,∴
,∴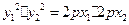 ,于是
,于是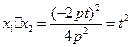 ,
,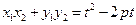 =
=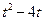
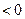 ,解得
,解得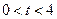 ,即
,即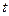 的取值范围是
的取值范围是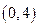 。
。
练习册系列答案
相关题目
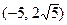
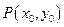 是
是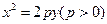 上的点,
上的点,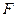 是抛物线的焦点,求证:
是抛物线的焦点,求证: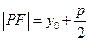 。
。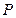 是抛物线
是抛物线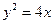 上一点,点
上一点,点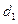 ,到直线
,到直线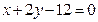 的距离为
的距离为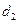 ,则
,则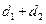 的最小值是( )
的最小值是( )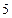


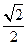
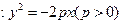 上横坐标为
上横坐标为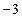 的一点,与其焦点的距离为4.(1)求
的一点,与其焦点的距离为4.(1)求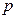 的值;(2)设动直线
的值;(2)设动直线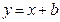 与抛物线C相交于A.B两点,问在直线
与抛物线C相交于A.B两点,问在直线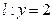 上是否存在与
上是否存在与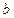 的取值无关的定点M,使得
的取值无关的定点M,使得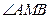 被直线
被直线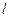 平分?若存在,求出点M的坐标;若不存在,说明理由.
平分?若存在,求出点M的坐标;若不存在,说明理由.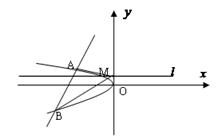
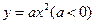 的焦点坐标和准线方程分别是( )
的焦点坐标和准线方程分别是( )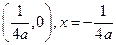
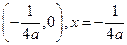
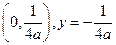
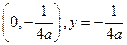
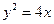 的一条弦
的一条弦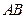 ,
,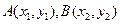 ,
,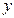 轴交于点
轴交于点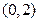 ,则
,则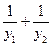 = 。
= 。