题目内容
设平面直角坐标系![]() 中,设二次函数
中,设二次函数![]() 的图像与两坐标轴有三个交点,经过这三个交点的圆记为
的图像与两坐标轴有三个交点,经过这三个交点的圆记为![]() 。求:
。求:
(1)求实数![]() 的取值范围。
的取值范围。
(2)求圆![]() 的方程。
的方程。
(3)问圆![]() 是否经过某定点(其坐标与
是否经过某定点(其坐标与![]() 无关)?请证明你的结论。
无关)?请证明你的结论。
解:本小题主要考查二次函数图象与性质、圆的方程的求法.
(Ⅰ)令![]() =0,得抛物线与
=0,得抛物线与![]() 轴交点是(0,b);
轴交点是(0,b);
令![]() ,由题意b≠0 且Δ>0,解得b<1 且b≠0.
,由题意b≠0 且Δ>0,解得b<1 且b≠0.
(Ⅱ)设所求圆的一般方程为![]()
![]()
令![]() =0 得
=0 得![]() 这与
这与![]() =0 是同一个方程,故D=2,F=
=0 是同一个方程,故D=2,F=![]() .
.
令![]() =0 得
=0 得![]() =0,此方程有一个根为b,代入得出E=b1.
=0,此方程有一个根为b,代入得出E=b1.
所以圆C 的方程为![]() .
.
(Ⅲ)圆C 必过定点(0,1)和(-2,1).
证明如下:将(0,1)代入圆C 的方程,得左边=0![]() +1
+1![]() +2×0-(b+1)+b=0,右边=0,
+2×0-(b+1)+b=0,右边=0,
所以圆C 必过定点(0,1).
同理可证圆C 必过定点(-2,1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

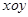 中,设二次函数
中,设二次函数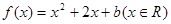 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: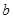 的取值范围;
的取值范围;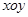 中,设二次函数
中,设二次函数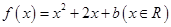 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为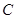 .求:
.求: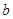 的取值范围;
的取值范围;