题目内容
(本小题满分12分)
设平面直角坐标系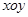 中,设二次函数
中,设二次函数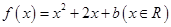 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为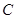 .求:
.求:
(Ⅰ)求实数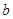 的取值范围;
的取值范围;
(Ⅱ)求圆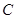 的方程;
的方程;
(Ⅲ)问圆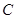 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
【答案】
(Ⅰ)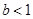 且
且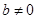
(Ⅱ)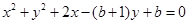
(Ⅲ)见解析
【解析】
试题分析:(Ⅰ)令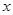 =0,得抛物线与
=0,得抛物线与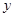 轴交点是
轴交点是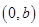 ;
;
令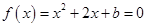 ,由题意
,由题意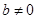 且Δ>0,
且Δ>0,
解得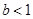 且
且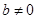 .
……2分
.
……2分
(Ⅱ)设所求圆的一般方程为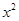
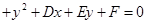 ,
,
令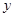 =0 得
=0 得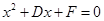 ,这与
,这与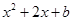 =0 是同一个方程,故
=0 是同一个方程,故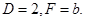
令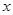 =0 得
=0 得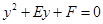 ,此方程有一个根为
,此方程有一个根为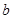 ,代入得出
,代入得出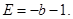
所以圆 的方程为
的方程为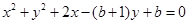 .
……6分
.
……6分
(Ⅲ)圆 必过定点
必过定点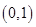 和
和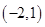 .
.
证明:法一:将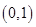 代入圆
代入圆 的方程,得左边=
的方程,得左边=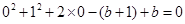 右边=
右边= ,
,
所以圆 必过定点
必过定点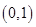 .
.
同理可证圆 必过定点
必过定点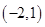 .
……12分
.
……12分
法二:圆 的方程为
的方程为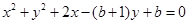 可化为
可化为
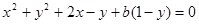
令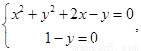 解得
解得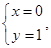 或
或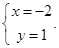
所以圆 必过定点
必过定点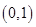 和
和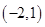 .
……12分
.
……12分
考点:本小题主要考查二次函数图象与性质、圆的方程的求法.
点评:由于圆的方程有两种形式:标准方程和一般方程,在做题时要合理选用,如果选择不恰当,可能会造成运算过于复杂而无法求解.

练习册系列答案
相关题目