题目内容
在平面直角坐标系xOy中,平面区域W中的点的坐标(x,y)满足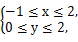 从区域W中随机取点M(x,y).
从区域W中随机取点M(x,y).
(1)若x∈Z,y∈Z,求点M位于第一象限的概率.
(2)若x∈R,y∈R,求|OM|≤2的概率.
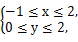 从区域W中随机取点M(x,y).
从区域W中随机取点M(x,y).(1)若x∈Z,y∈Z,求点M位于第一象限的概率.
(2)若x∈R,y∈R,求|OM|≤2的概率.
(1) (2)
(2) π+
π+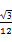
 (2)
(2) π+
π+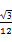
(1)若x,y∈Z,则点M的个数共有12个,列举如下:(-1,0),(-1,1),(-1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),
(2,1),(2,2).
当点M的坐标为(1,1),(1,2),(2,1),(2,2)时,点M位于第一象限,
故点M位于第一象限的概率为 .
.
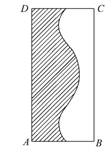
(2)如图:
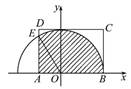
若x,y∈R,则区域W的面积是3×2=6.
满足|OM|≤2的点M构成的区域为{(x,y)|-1≤x≤2,0≤y≤2,x2+y2≤4},即图中的阴影部分.易知E(-1,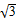 ),∠EOA=60°,
),∠EOA=60°,
所以扇形BOE的面积是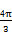 ,△EAO的面积是
,△EAO的面积是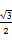 .
.
所以|OM|≤2的概率为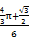 =
= π+
π+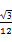 .
.
(2,1),(2,2).
当点M的坐标为(1,1),(1,2),(2,1),(2,2)时,点M位于第一象限,
故点M位于第一象限的概率为
 .
.(2)如图:

若x,y∈R,则区域W的面积是3×2=6.
满足|OM|≤2的点M构成的区域为{(x,y)|-1≤x≤2,0≤y≤2,x2+y2≤4},即图中的阴影部分.易知E(-1,
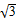 ),∠EOA=60°,
),∠EOA=60°,所以扇形BOE的面积是
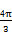 ,△EAO的面积是
,△EAO的面积是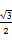 .
.所以|OM|≤2的概率为
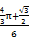 =
= π+
π+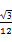 .
.
练习册系列答案
相关题目

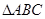 内部随机取一点
内部随机取一点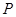 ,则事件“
,则事件“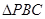 的面积不大于
的面积不大于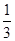 ”的概率是
”的概率是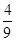
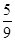
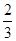
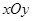 中,不等式组
中,不等式组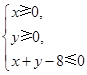 所表示的平面区域是
所表示的平面区域是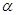 ,不等式组
,不等式组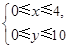 所表示的平面区域是
所表示的平面区域是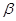 . 从区域
. 从区域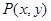 ,则P为区域
,则P为区域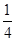
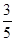
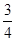
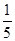
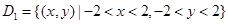 ,
,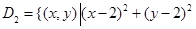
 .在区域
.在区域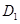 内随机选取一点区域
内随机选取一点区域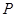 ,则点
,则点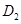 的概率是
的概率是