题目内容
已知椭圆C的方程为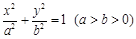 ,其离心率为
,其离心率为 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l: 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足 ,求
,求 的取值范围.
的取值范围.
【答案】
(Ⅰ)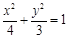 .
(Ⅱ)
.
(Ⅱ) 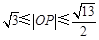 。
。
【解析】
试题分析:(Ⅰ)由已知可得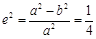 ,
,
所以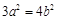
又 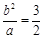
解之得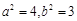
故椭圆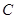 的方程为
的方程为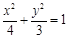 . 5分
. 5分
(Ⅱ)
由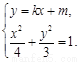 消y化简整理得:
消y化简整理得: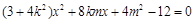 ,
,
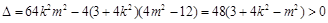 ①
①
设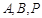 点的坐标分别为
点的坐标分别为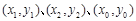 ,
,
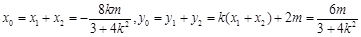 8分
8分
由于点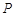 在椭圆
在椭圆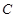 上,所以
上,所以
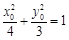 .
.
从而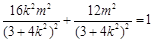 ,化简得
,化简得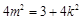 ,经检验满足①式.
,经检验满足①式.
又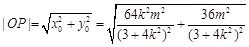
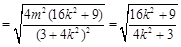
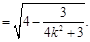
因为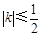 ,得3≤4k2+3≤4,
,得3≤4k2+3≤4,
有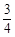 ≤
≤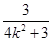 ≤1,故
≤1,故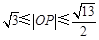 12分
12分
考点:椭圆的标准方程,平面向量的线性运算,直线与椭圆的位置关系。
点评:中档题,确定圆锥曲线的标准方程,往往利用几何特征,确定a,b,c,e得到关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题利用韦达定理,简化了计算过程。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目