题目内容
(原创)若对定义在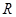 上的可导函数
上的可导函数 ,恒有
,恒有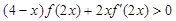 ,(其中
,(其中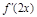 表示函数
表示函数 的导函数
的导函数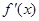 在
在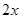 的值),则
的值),则 ( )
( )
| A.恒大于等于0 | B.恒小于0 |
| C.恒大于0 | D.和0的大小关系不确定 |
C
解析试题分析:函数 ,则
,则 =
=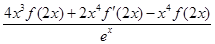 =
=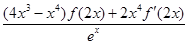 =
=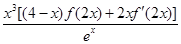 ,∵
,∵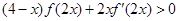 恒成立,∴当
恒成立,∴当 时,
时, ,此时函数
,此时函数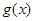 单调递增;当
单调递增;当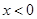 时,
时, ,此时函数
,此时函数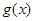 单调递减,∴当
单调递减,∴当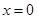 时,
时,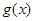 取得极小值,同时也是最小值
取得极小值,同时也是最小值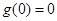 ,∴
,∴ ,即
,即 .当
.当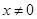 时,
时,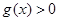 ,∴当
,∴当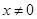 时,
时,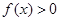 .∵
.∵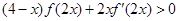 恒成立,∴当
恒成立,∴当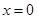 时,
时,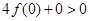 恒成立,∴
恒成立,∴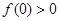 .综上无论
.综上无论 取何值,恒有
取何值,恒有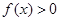 ,故选C.
,故选C.
考点:1、导数的应用;2、不等式性质.

练习册系列答案
相关题目
曲线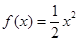 在点
在点 处的切线方程为( )
处的切线方程为( )
A.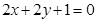 | B.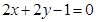 |
C.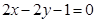 | D.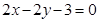 |
定义在R上的函数 满足
满足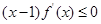 ,且
,且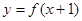 为偶函数,当
为偶函数,当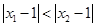 时,有( )
时,有( )
A.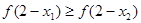 | B.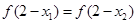 |
C.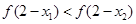 | D.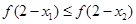 |
由曲线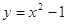 ,直线
,直线 ,
, 和
和 轴围成的封闭图形的面积(如图)可表示为( )
轴围成的封闭图形的面积(如图)可表示为( )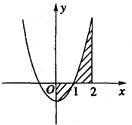
A. | B.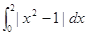 |
C. | D.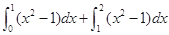 |
可导函数 的导函数为
的导函数为 ,且满足:①
,且满足:① ;②
;② ,记
,记 ,
,  ,
, 则
则 的大小顺序为( )
的大小顺序为( )
A. | B. | C. | D. |
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
| A.(-2,+∞) | B.(0,+∞) |
| C.(1,+∞) | D.(4,+∞) |
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo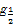 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
| A.是增函数,且f(x)<0 |
| B.是增函数,且f(x)>0 |
| C.是减函数,且f(x)<0 |
| D.是减函数,且f(x)>0 |
已知函数f(x)=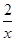 +xln x,则曲线y=f(x)在x=1处的切线方程为( )
+xln x,则曲线y=f(x)在x=1处的切线方程为( )
| A.x-y-3=0 | B.x-y+3=0 | C.x+y-3=0 | D.x+y+3=0 |
过曲线y=x3+x-2上一点P0处的切线平行于直线y=4x,则点P0的一个坐标是( )
| A.(0,-2) | B.(1,1) | C.(1,4) | D.(-1,-4) |