题目内容
曲线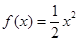 在点
在点 处的切线方程为( )
处的切线方程为( )
A.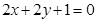 | B.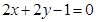 |
C.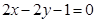 | D.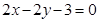 |
C
解析试题分析: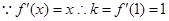 ,因此曲线
,因此曲线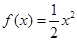 在点
在点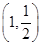 处的切线方程为
处的切线方程为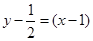 ,即
,即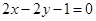
考点:利用导数求切线方程

练习册系列答案
相关题目
由曲线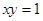 ,直线
,直线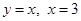 所围成封闭的平面图形的面积为 ( )
所围成封闭的平面图形的面积为 ( )
A.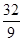 | B.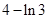 | C.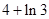 | D.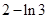 |
下列求导运算正确的是( )
A.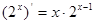 | B.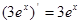 |
C.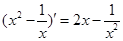 | D.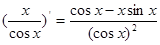 |
(原创)若对定义在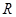 上的可导函数
上的可导函数 ,恒有
,恒有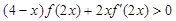 ,(其中
,(其中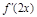 表示函数
表示函数 的导函数
的导函数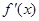 在
在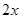 的值),则
的值),则 ( )
( )
| A.恒大于等于0 | B.恒小于0 |
| C.恒大于0 | D.和0的大小关系不确定 |
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A.-1 | B.1 | C.±1 | D.-2 |
若存在x使不等式 >
>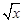 成立,则实数m的取值范围为( )
成立,则实数m的取值范围为( )
A.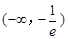 | B. | C. | D. |
物体A以v=3t2+1(m/s)的速度在一直线l上运动,物体B在直线l上,且在物体A的正前方5m处,同时以v=10t(m/s)的速度与A同向运动,出发后物体A追上物体B所用的时间t(s)为( )
| A.3 | B.4 | C.5 | D.6 |
设函数f(x)=ex+x-2,g(x)=ln x+x2-3.若实数a,b满足f(a)=0,g(b)=0,则 ( ).
| A.g(a)<0<f(b) | B.f(b)<0<g(a) |
| C.0<g(a)<f(b) | D.f(b)<g(a)<0 |
由直线x=-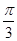 ,x=
,x=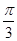 ,y=0与曲线y=cos x围成的封闭图形的面积为( ).
,y=0与曲线y=cos x围成的封闭图形的面积为( ).
A. | B.1 | C.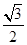 | D. |