题目内容
已知一个圆的圆心为坐标原点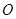 ,半径为
,半径为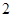 .从这个圆上任意一点
.从这个圆上任意一点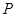 向
向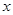 轴作垂线
轴作垂线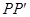 ,
,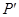 为垂足.
为垂足.
(Ⅰ)求线段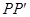 中点
中点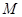 的轨迹方程;
的轨迹方程;
(Ⅱ)已知直线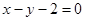 与
与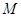 的轨迹相交于
的轨迹相交于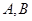 两点,求
两点,求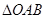 的面积
的面积
(1) ;(2)
;(2)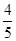 .
.
解析试题分析:(1)本题一般用动点转移法求轨迹方程,设动点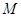 的坐标为
的坐标为 ,则点
,则点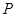 的坐标为
的坐标为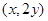 ,而点
,而点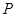 又是已知圆的点,把
又是已知圆的点,把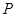 点坐标代入圆的方程即能求出动点
点坐标代入圆的方程即能求出动点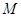 的轨迹方程;(2)直接列方程组求出交点
的轨迹方程;(2)直接列方程组求出交点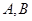 的坐标,然后选用相应面积公式计算面积(本题中以OB为底,高就是点A的纵坐标的绝对值).
的坐标,然后选用相应面积公式计算面积(本题中以OB为底,高就是点A的纵坐标的绝对值).
试题解析:(1)设 ,
,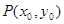 则
则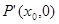 1分
1分
由中点公式得: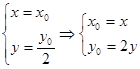 3分
3分
因为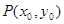 在圆上,
在圆上,
∴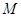 的轨迹方程为
的轨迹方程为 6分
6分
(2)据已知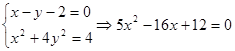 8分
8分 10分
10分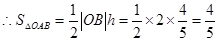 12分
12分
考点:(1)动点转移法求轨迹方程;(2)三角形的面积.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
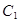 上任意一点
上任意一点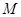 到直线
到直线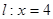 的距离是它到点
的距离是它到点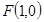 距离的
距离的 倍;曲线
倍;曲线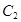 是以原点为顶点,
是以原点为顶点,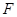 为焦点的抛物线.
为焦点的抛物线.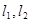 ,其中
,其中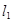 与
与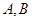 ,
,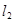 与
与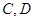 ,求四边形
,求四边形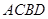 面积的取值范围.
面积的取值范围. :
: 的离心率为
的离心率为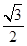 ,以椭圆
,以椭圆 为圆心作圆
为圆心作圆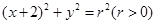 ,设圆
,设圆 与点
与点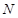 .(12分)
.(12分)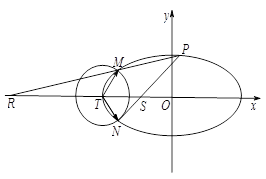
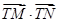 的最小值,并求此时圆
的最小值,并求此时圆 是椭圆
是椭圆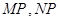 分别与
分别与 轴交于点
轴交于点 ,
,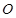 为坐标原点,求证:
为坐标原点,求证: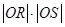 为定值.(5分)
为定值.(5分)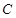 的顶点为原点,其焦点
的顶点为原点,其焦点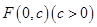 到直线
到直线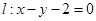 的距离为
的距离为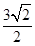 .设
.设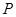 为直线
为直线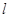 上的点,过点
上的点,过点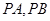 ,其中
,其中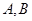 为切点.
为切点.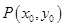 为直线
为直线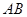 的方程;
的方程;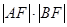 的最小值.
的最小值.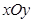 中,点
中,点 为动点,
为动点,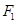 、
、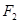 分别为椭圆
分别为椭圆 的左、右焦点.已知
的左、右焦点.已知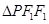 为等腰三角形.
为等腰三角形.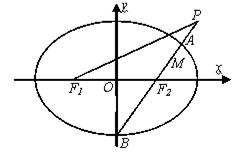
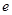 ;
;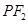 与椭圆相交于
与椭圆相交于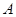 、
、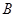 两点,
两点,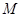 是直线
是直线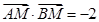 ,求点
,求点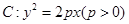 的焦点为
的焦点为 ,准线为
,准线为 ,
,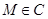 ,以
,以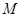 为圆心的圆
为圆心的圆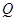 ,
,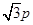 ,
,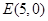 是圆
是圆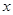 轴除
轴除 与圆
与圆 的直线
的直线 与
与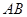 两点,求
两点,求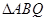 的面积.
的面积.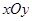 中,直线l与抛物线
中,直线l与抛物线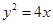 相交于不同的两点A,B.
相交于不同的两点A,B.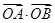 的值;
的值;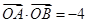 ,证明直线l必过一定点,并求出该定点坐标.
,证明直线l必过一定点,并求出该定点坐标.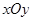 中,已知椭圆
中,已知椭圆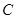 :
: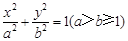 的离心率
的离心率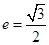 ,且椭圆C上一点
,且椭圆C上一点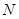 到点Q
到点Q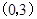 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆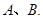
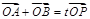 (O为坐标原点),当
(O为坐标原点),当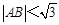 时,求实数
时,求实数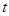 的取值范围.
的取值范围.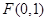 且与直线
且与直线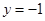 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为 .点
.点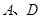 在轨迹
在轨迹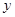 轴对称,过线段
轴对称,过线段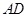 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线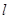 ,使直线
,使直线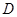 处的切线平行,设直线
处的切线平行,设直线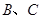 .
.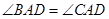 ;
;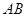 的距离等于
的距离等于 ,且
,且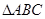 的面积为20,求直线
的面积为20,求直线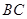 的方程.
的方程.