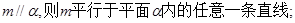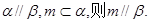题目内容
如图,四边形ABCD为正方形,PA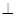 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
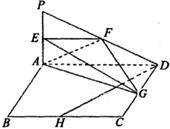
(I)求证:BC∥平面EFG;
(II)求证:DH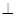 平面AEG.
平面AEG.
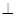 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(I)求证:BC∥平面EFG;
(II)求证:DH
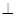 平面AEG.
平面AEG.(Ⅰ)见解析;(Ⅱ)见解析.
试题分析:(Ⅰ)根据
 分别为
分别为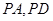 中点,得到
中点,得到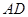 ∥
∥ ,
,根据
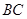 ∥
∥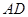 ,推出
,推出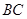 ∥
∥ 即得证.
即得证.(Ⅱ)由
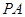 ⊥平面
⊥平面 ,得到
,得到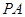 ⊥
⊥ ,即
,即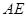 ⊥
⊥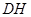 ;
;再利用△
 ≌△
≌△ ,可推出∠
,可推出∠ =∠
=∠ ,∠
,∠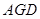 +∠
+∠ =90°,得到∠
=90°,得到∠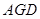 +∠
+∠ =90°,证得
=90°,证得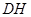 ⊥
⊥ 后即得证.
后即得证.试题解析:(Ⅰ)因为
 分别为
分别为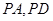 中点,所以
中点,所以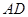 ∥
∥ ,
,因为
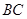 ∥
∥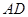 ,所以
,所以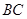 ∥
∥ , 2分
, 2分因为
 平面
平面 平面
平面 , 4分
, 4分所以
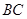 ∥平面
∥平面 . 6分
. 6分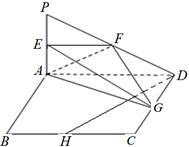
(Ⅱ)因为
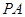 ⊥平面
⊥平面 ,所以
,所以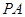 ⊥
⊥ ,
,即
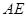 ⊥
⊥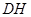 , 8分
, 8分因为△
 ≌△
≌△ ,
,所以∠
 =∠
=∠ ,
,∠
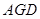 +∠
+∠ =90°,
=90°,所以∠
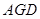 +∠
+∠ =90°,
=90°,所以
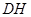 ⊥
⊥ ,
,又因为
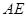 ∩
∩ =
= ,所以
,所以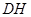 ⊥平面
⊥平面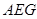 . 12分
. 12分
练习册系列答案
相关题目
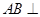 平面
平面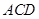 ,
,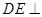 平面
平面 ,△
,△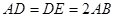 ,
,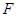 为
为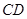 的中点.
的中点.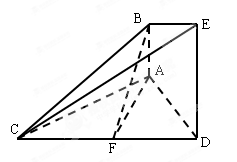
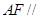 平面
平面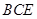 ;
;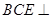 平面
平面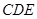 .
.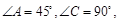
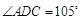 ,
,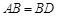 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD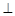 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

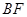 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 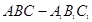 中,
中,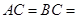
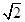 ,且
,且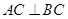 ,点
,点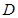 是
是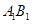 中点.
中点.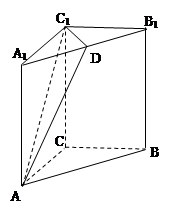
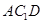 ⊥平面
⊥平面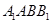 ;
;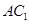 与平面
与平面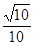 ,
,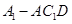 的体积.
的体积.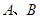 为正方体的两个顶点,
为正方体的两个顶点,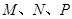 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出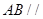 平面
平面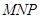 的图形的序号是( )
的图形的序号是( )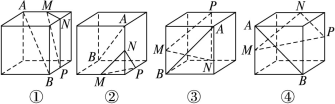
 都在平面
都在平面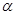 外, 则下列推断错误的是( )
外, 则下列推断错误的是( )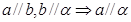
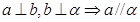
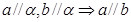
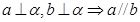
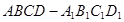 中,
中,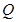 是
是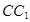 的中点,
的中点,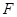 是侧面
是侧面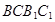 内的动点且
内的动点且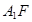 //平面
//平面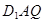 ,则
,则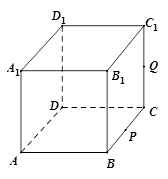
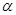 、
、 是两个不同的平面,
是两个不同的平面,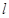 是一条直线,以下命题:
是一条直线,以下命题: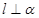 ,
,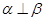 ,则
,则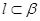 ;②若
;②若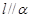 ,
,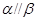 ,则
,则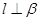 ;④若
;④若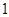



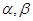 是不重合的平面,下列命题正确的是( ):
是不重合的平面,下列命题正确的是( ):