题目内容
已知函数
(1)若函数y=f(x)的图象切x轴于点(2,0),求a、b的值;
(2)设函数y="f(x)"  的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;(3)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证
的充要条件;(3)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证 。
。
(1) ,
, ;(2)
;(2)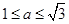 ;(3))设
;(3))设 则
则 =
= ,即
,即 ,对
,对 恒成立,
恒成立,
 ,对
,对 恒成立即
恒成立即 对
对 恒成立,解得
恒成立,解得
解析试题分析:(1)

由 得
得 ,
,
又 得
得 …………………………2分
…………………………2分
(2) k=
k=
 ,
, 对任意的
对任意的
 ,即
,即 对任意的
对任意的 恒成立……3分
恒成立……3分
等价于 对任意的
对任意的 恒成立。…………………………4分
恒成立。…………………………4分
令g(x)= ,h(x)=
,h(x)= ,
,
则 ,
, ………………………………5分
………………………………5分 ,当且仅当
,当且仅当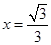 时“=”成立,
时“=”成立,
 …………6分
…………6分 h(x)=
h(x)= 在(0,1)上为增函数,
在(0,1)上为增函数, h(x)max<2 ……………………7分
h(x)max<2 ……………………7分
所以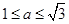 …………………………………………………………………8分
…………………………………………………………………8分
(3)设 则
则 =
= ……9分
……9分
即 ,对
,对 恒成立 ……………………10分
恒成立 ……………………10分
 ,对
,对 恒成立
恒成立
即 对
对 恒成立 ……………………11分
恒成立 ……………………11分

解得 …………………12分
…………………12分
考点:导数的几何意义;利用倒数研究曲线的切线方程;
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及导数的几何意义,同时考查了恒成立问题和转化的数学思想,是一道综合题,有一定的难点.

练习册系列答案
相关题目
 .
. 的单调递增区间;
的单调递增区间; 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.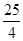 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围. 。
。 时,求函数
时,求函数 的最小值;
的最小值; 时,求实数
时,求实数 的取值范围。
的取值范围。 。
。 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围。
的取值范围。 的导函数为
的导函数为 ,且
,且 。
。 的图象在x=0处的切线方程;
的图象在x=0处的切线方程; 为奇函数,a为常数。
为奇函数,a为常数。 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 的表达式,并判断
的表达式,并判断 时,恒有
时,恒有 求m的取值范围。
求m的取值范围。