题目内容
直线 截圆x2+y2=4得的劣弧所对的圆心角是( )
截圆x2+y2=4得的劣弧所对的圆心角是( )
A. | B. | C. | D. |
C
解析试题分析:设圆心为C,可得C到直线 的距离为
的距离为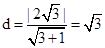 ,
,
Rt△AMC中,半径AC=2,可得cos∠ACM=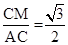 ,
,
所以,∠ACM=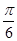 ,由垂径定理得,圆心角∠ACB=2∠ACM=
,由垂径定理得,圆心角∠ACB=2∠ACM=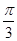 ,故选C.
,故选C.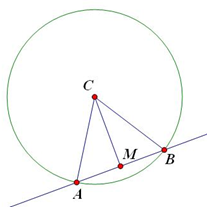
考点:直线与圆的位置关系
点评:中档题,利用数形结合的思想,运用垂径定理解决直线与圆相交所成的圆心角大小问题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以双曲线 的右焦点为圆心,且与其渐近线相切的圆的方程是( )
的右焦点为圆心,且与其渐近线相切的圆的方程是( )
A. | B. |
C.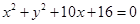 | D. |
圆 在点
在点 处的切线方程为( )
处的切线方程为( )
A. | B. |
C. | D. |
直线l:y=kx-3k与圆C:x +y
+y -4x=0的位置关系是
-4x=0的位置关系是
| A.l与C相交 | B.l与C相切 |
| C.l与C相离 | D.以上三个选项均有可能 |
自点  的切线,则切线长为( )
的切线,则切线长为( )
A. | B.3 | C. | D.5 |
过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是( )
A.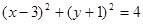 | B.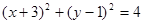 |
C.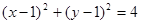 | D.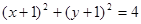 |
圆心为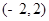 ,半径为5的圆的标准方程为( )
,半径为5的圆的标准方程为( )
A.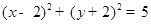 | B.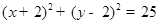 |
C.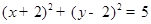 | D.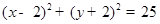 |
已知过点P(2,2) 的直线与圆 相切, 且与直线
相切, 且与直线 垂直, 则
垂直, 则 ( )
( )
A. | B.1 | C.2 | D. |
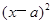 +
+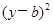 =
=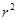 (ab≠0,r>0)的图像可能是
(ab≠0,r>0)的图像可能是