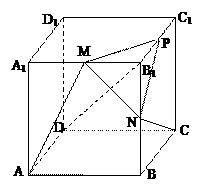题目内容
如图,平面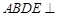 平面
平面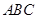 ,
,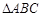 是等腰直角三角形,
是等腰直角三角形,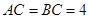 ,四边形
,四边形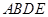 是直角梯形,
是直角梯形,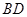 ∥AE,
∥AE,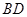
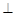
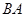 ,
,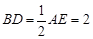 ,
,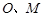 分别为
分别为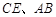 的中点.
的中点.
(1)求异面直线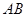 与
与 所成角的大小;
所成角的大小;
(2)求直线 和平面
和平面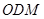 所成角的正弦值.
所成角的正弦值.
(1)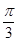 ,(2)
,(2)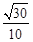
解析试题分析:(1)求空间角,一般利用空间向量解决.首先要建立恰当的空间直角坐标系,由平面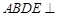 平面
平面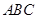 及
及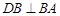 ,运用面面垂直性质定理,可得
,运用面面垂直性质定理,可得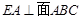 ,这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线
,这样确定竖坐标.横坐标与纵坐标可根据右手系建立.因为异面直线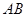 与
与 所成角
所成角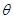 等于向量
等于向量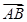 与
与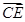 夹角或其补角,而异面直线
夹角或其补角,而异面直线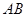 与
与 所成角范围为
所成角范围为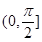 ,所以
,所以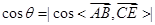 ,(2) 直线
,(2) 直线 和平面
和平面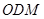 所成角
所成角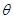 与向量
与向量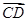 与平面
与平面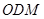 法向量
法向量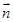 夹角互余或相差
夹角互余或相差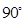 ,而直线
,而直线 和平面
和平面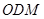 所成角
所成角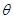 范围为
范围为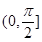 ,所以
,所以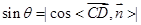 .
.
试题解析:
∵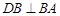 ,又∵面
,又∵面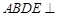 面
面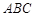 ,面
,面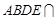 面
面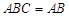 ,
, ,∴
,∴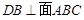 ,∵BD∥AE,∴
,∵BD∥AE,∴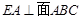 , 2分
, 2分
如图所示,以C为原点,分别以CA,CB为x,y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,∵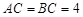 ,∴设各点坐标为
,∴设各点坐标为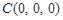 ,
,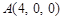 ,
, ,
, ,
,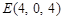 ,
,
则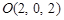 ,
,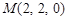 ,
,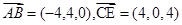 ,
,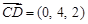 ,
,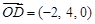 ,
,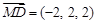 .
.
(1)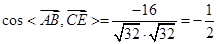 ,
,
则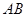 与
与 所成角为
所成角为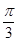 . 5分
. 5分
(2)设平面ODM的法向量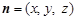 ,则由
,则由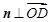 ,且
,且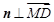 可得
可得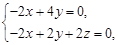
令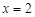 ,则
,则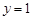 ,
,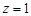 ,∴
,∴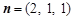 ,设直线CD和平面ODM所成角为
,设直线CD和平面ODM所成角为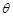 ,则
,则 ,
,
∴直线CD和平面ODM所成角的正弦值为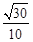 . 10分
. 10分
考点:利用空间向量求异面直线所成角及直线与平面所成角.

练习册系列答案
相关题目
 ·
· .
.
 PD.
PD.
 ,求
,求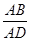 的值.
的值.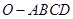 中,底面
中,底面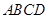 是边长为
是边长为 的菱形,
的菱形,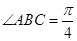 ,
,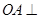 底面
底面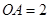 ,
,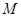 为
为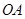 的中点,
的中点,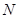 为
为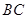 的中点.
的中点.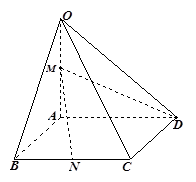
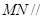 平面
平面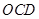 ;
;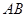 与
与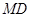 所成角的大小;
所成角的大小; 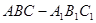 的所有棱长都为4,D为的
的所有棱长都为4,D为的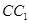 中点.
中点.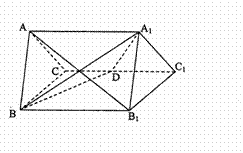
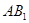 ⊥平面
⊥平面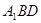 ;
;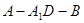 余弦值.
余弦值. ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的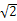 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.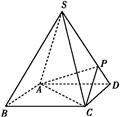
 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面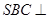 面
面
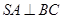 ;
;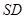 与面
与面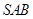 所成角的正弦值。
所成角的正弦值。
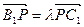 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求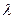 的值.
的值.