题目内容
15.已知log142=a,用a表示log${\;}_{\sqrt{2}}$7.分析 由已知条件利用换底公式得到$\frac{2}{2+lo{g}_{\sqrt{2}}7}$=a,由此能用a表示log${\;}_{\sqrt{2}}$7.
解答 解:∵log142=a,
∴log142=$\frac{lo{g}_{\sqrt{2}}2}{lo{g}_{\sqrt{2}}14}$=a,
∴$\frac{2lo{g}_{\sqrt{2}}\sqrt{2}}{lo{g}_{\sqrt{2}}2+lo{g}_{\sqrt{2}}7}$=a,
∴$\frac{2}{2+lo{g}_{\sqrt{2}}7}$=a,
∴2a+a$lo{g}_{\sqrt{2}}7$=2,
∴a$lo{g}_{\sqrt{2}}$7=2-2a,
∴log${\;}_{\sqrt{2}}$7=$\frac{2-2a}{a}$.
点评 本题考查对数式的化简求值,是基础题,解题时要认真审题,注意换底公式的合理运用.

练习册系列答案
相关题目
10.若对于任意实数x∈[e,e2],不等式$\frac{{e}^{m}}{2}$>x-$\frac{{e}^{2}}{lnx}$恒成立,则实数的取值范围是 ( )
| A. | (-∞,-2) | B. | (-∞,2) | C. | ($\frac{1}{2}$,+∞) | D. | (2,+∞) |
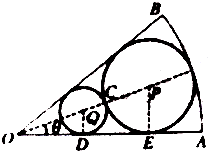 如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.
如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.