题目内容
10.已知y=f(x)是定义在R上的奇函数,当x≤0时,f(x)=x-x2.(1)求x>0时,f(x)的解析式;
(2)问是否存在这样的正实数a,b,当x∈[a,b]时,f(x)的值域为[4a-2,6b-6]?若存在,求出所有的a,b值;若不存在,请说明理由.
分析 (1)根据f(x)为奇函数,可设x>0,从而-x<0,从而f(-x)=-x-x2=-f(x),解出f(x)即可得出x>0时的f(x)的解析式;
(2)由上面x>0时,f(x)=x2+x,从而可判断此时f(x)在(0,+∞)上单调递增,从而可根据题意有$\left\{\begin{array}{l}{f(a)=4a-2}\\{f(b)=6b-6}\end{array}\right.$,这样解出a,b,并满足a<b,即可找出所有的a,b值.
解答 解:(1)设x>0,则-x<0,于是f(-x)=-x-x2;
又f(x)为奇函数,即f(-x)=-f(x);
即x>0时,f(x)=x+x2;
(2)假设存在这样的数a,b;
∵a>0,且f(x)=x+x2在x>0时为增函数;
∴x∈[a,b]时,f(x)∈[f(a),f(b)]=[4a-2,6b-6];
∴$\left\{\begin{array}{l}{{a}^{2}+a=4a-2}\\{{b}^{2}+b=6b-6}\end{array}\right.$;
解得$\left\{\begin{array}{l}{b=2,或3}\\{a=1,或2}\end{array}\right.$;
即$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,或$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$,或$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,或$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$;
∵a<b;
∴a,b的取值为$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,或$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$,或$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$.
点评 考查奇函数的定义,二次函数的单调性,以及增函数在闭区间上的值域求法,注意条件a<b.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案 某种产品的广告费用x与销售额y的统计数据如下表:
某种产品的广告费用x与销售额y的统计数据如下表:| 广告费用x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 10 | 12 | 15 | 18 | 20 |
(2)预计在今后的销售中,销售额与广告费用还服从(1)中的关系,如果广告费用为6万元,请预测销售额为多少万元?
附:其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 | 男 | 女 |
| 需要 | 80 | 60 |
| 不需要 | 320 | 540 |
(2)能否在犯错误的概率不超过0.001的前提下,认为该市外来务工人员春节买票回家是否需要交通部门提供帮助与性别有关?
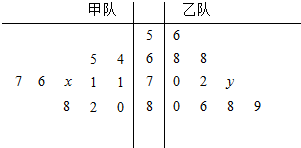 如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
如图的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.