题目内容
某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了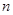 人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) |  | 0.5 |
| 第2组 | [25,35) | 18 |  |
| 第3组 | [35,45) |  | 0.9[ |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 |  |

(1)分别求出
 的值;
的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
(1)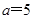 ,
,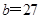 ,
,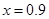 ,
,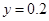 ;(2) 第2组2人,第3组3人,第4组1人;(3)
;(2) 第2组2人,第3组3人,第4组1人;(3) 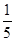 .
.
解析试题分析:(1)利用第4小组的数据,先求出样本容量,然后分别求出 的值;(2)利用分层抽样的定义,进行抽取;(3)利用古典概型的概率公式求概率.
的值;(2)利用分层抽样的定义,进行抽取;(3)利用古典概型的概率公式求概率.
(1)由频率表中第4组数据可知,第4组总人数为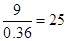 ,
,
再结合频率分布直方图可知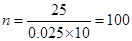 ,
,
∴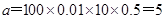 ,
,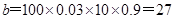 ,
,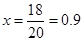 ,
,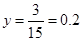 .
.
(2)第2,3,4组回答正确的共有54人.
∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组: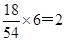 人,第3组:
人,第3组: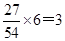 人,第4组:
人,第4组: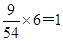 人.
人.
(3)设所抽取的人中第2组的2人为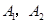 ;第3组的3人为
;第3组的3人为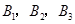 ;第4组的1人为
;第4组的1人为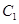 ,
,
则从6人中抽2人所有可能的结果有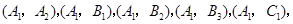
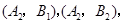
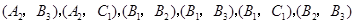 ,
,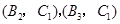 ,共15个基本事件,其中恰好没有第3组人共3个基本事件,
,共15个基本事件,其中恰好没有第3组人共3个基本事件,
∴所抽取的人中恰好没有第3组人的概率为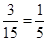 .
.
考点:1、分层抽样;2、频率分布直方图;3、古典概型.

练习册系列答案
相关题目
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
 | 2 | 3 | 4 | 5 | 6 |
 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
 ,
, ,
,(1)在下面坐标系中画出散点图;

(2)计算
 ,
, ,并求出线性回归方程;
,并求出线性回归方程;(3)在第(2)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少?
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
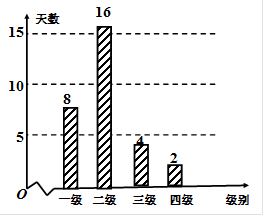
某市2013年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如下条形图:
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率.
为了对新产品进行合理定价,对该产品进行了试销试验,以观察需求量Y(单位:千件)对于价格x(单位:千元)的反应,得数据如下:
| x/千元 | 50 | 70 | 80 | 40 | 30 | 90 | 95 | 97 |
| y/千件 | 100 | 80 | 60 | 120 | 135 | 55 | 50 | 48 |
(2)若成本x=y+500,试求:
①在盈亏平衡条件下(利润为零)的价格;
②在利润为最大的条件下,定价为多少?
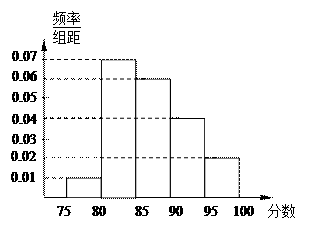
 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。

 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当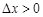 时,称本月价格指数环比增长;
时,称本月价格指数环比增长; 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.