题目内容
.一质点做直线运动,其瞬时加速度的变化规律为a(t)=-A ω2cost,在t=0时,v(0)=0,s(0)=A,其中A、ω为常数,求质点的位移方程.
质点的位移方程为s(t)=A ω2cost+A-Aω2,t∈[0,+∞).
v(t)-v(0)= ,
,
∴v(t)=-Aω2sint| =-Aω2sint.
=-Aω2sint.
∴s(t)-s(0)= ,
,
s(t)-A=Aω2cost-Aω2.
∴s(t)=A+A ω2cost-Aω2.
∴质点的位移方程为s(t)=A ω2cost+A-Aω2,t∈[0,+∞).
 ,
,∴v(t)=-Aω2sint|
 =-Aω2sint.
=-Aω2sint.∴s(t)-s(0)=
 ,
,s(t)-A=Aω2cost-Aω2.
∴s(t)=A+A ω2cost-Aω2.
∴质点的位移方程为s(t)=A ω2cost+A-Aω2,t∈[0,+∞).

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 g
g g
g 的图象与
的图象与 轴所围成的图形的面积为 .
轴所围成的图形的面积为 . ,则当
,则当 时,定积分
时,定积分 的符号
的符号  时是正的,当
时是正的,当 时是负的
时是负的 ,直线
,直线 ,
, 和
和 轴围成的封闭图形的面积是 ( )
轴围成的封闭图形的面积是 ( )



 ,当
,当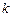 = 时,
= 时,  .恒成立
.恒成立