题目内容
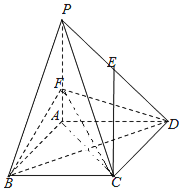
【题目】如图所示，在底面为正方形的四棱锥P—ABCD中，AB=2，PA=4，PB=PD=
，AC与BD相交于点O，E，G分别为PD，CD中点，
(1)求证：EO//平面PBC；
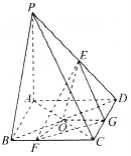
(2)设线段BC上点F满足BC=3BF，求三棱锥E—OFG的体积．
【答案】（1）见解析（2）
【解析】
(1)由EO//PB，可证EO//平面PBC；
（2）由勾股定理可证PA⊥AB,且PA⊥AD,故PA⊥面ABCD，E到底面的距离等于P点到底面距离的一半，再求出△FOG的面积，利用体积计算公式即可求解.
（1）证明：
E为PD中点，O为BD中点，
EO 为△PBD中位线，EO//PB ,又
,
, EO//平面PBC.
（2） AB=2，PA=4，PB=PD=
，
,
,同理可得
.
又
,
面ABCD，
故P到面ABCD的距离为4，E到面ABCD的距离
练习册系列答案
相关题目
【题目】某高校随机抽取部分男生测试立定跳远，将成绩整理得到频率分布表如表，测试成绩在220厘米以上（含220厘米）的男生定为“合格生”，成绩在260厘米以上（含260厘米）的男生定为“优良生”．
分组（厘米） | 频数 | 频率 |
[180，200） | 0.10 | |
[200，220） | 15 | |
[220，240） | 0.30 | |
[240，260） | 0.30 | |
[260，280） | 0.20 | |
合计 | 1.00 |
（1）求参加测试的男生中“合格生”的人数．
（2）从参加测试的“合格生”中，根据表中分组情况，按分层抽样的方法抽取8名男生，再从这8名男生中抽取3名男生，记X表示3人中“优良生”的人数，求X的分布列及数学期望．
