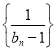题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,
,![]() 有且只有
有且只有![]() 个零点,求实数
个零点,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
,![]() ,
,![]() ,求正整数
,求正整数![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)![]() (3)2
(3)2
【解析】
(1)将![]() 代入,求导后根据单调性求出函数
代入,求导后根据单调性求出函数![]() 的最大值,即可证明;
的最大值,即可证明;
(2)由![]() 有且只有
有且只有![]() 个零点,对
个零点,对![]() 分类讨论,得
分类讨论,得![]() 的极大值大于
的极大值大于![]() ,得出实数
,得出实数![]() 的取值范围,再根据(1)验证由
的取值范围,再根据(1)验证由![]() 有且只有
有且只有![]() 个零点即可;
个零点即可;
(3)构造函数![]() ,根据
,根据![]() ,求出函数
,求出函数![]() 的最大值
的最大值![]() ,再代入
,再代入![]() ,即可得到正整数
,即可得到正整数![]() 的最小值
的最小值
(1)由题知,![]() ,
,![]() ,
,
所以,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() ;
;
(2)因为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,不可能有
上单调递增,不可能有![]() 个零点,
个零点,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
所以,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() ,
,
若![]() 只有
只有![]() 个零点,则
个零点,则![]() ,解得:
,解得:![]() ,
,
由(1)知:![]() ,所以
,所以![]() ,令
,令![]() ,
,
解得:![]() 或
或![]() ,
,
所以,存在![]() ,满足
,满足![]() ;
;
存在![]() ,满足
,满足![]() ;
;
所以![]() 在
在![]() 和
和![]() 上个恰有
上个恰有![]() 个零点,符合题意,
个零点,符合题意,
综上,所求实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)令![]() ,
,
所以![]() ,
,
![]()
![]() ,
,![]()
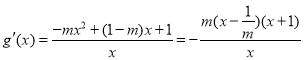 .
.
令![]() ,得
,得![]() ,所以当
,所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 是减函数,
是减函数,
所以![]() ,
,
令![]() ,因为
,因为![]() ,
,![]() ,
,
又因为![]() 在
在![]() 上是减函数,所以当
上是减函数,所以当![]() 时,
时,![]() ,
,
所以整数![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如表
评估的平均得分 | (0,6] | (6,8] | (8,10] |
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级.
(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超0.5的概率.