题目内容
已知函数![]() ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值x1,x2,都有![]() ,求实数c的最小值;
,求实数c的最小值;
(3)若过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,求实数m的取值范围.
答案:
解析:
解析:
|
解:(1) 根据题意,得 ∴f(x)=x3-3x 4分 (2)令
∵f(-1)=2,f(1)=-2,∴当x∈[-2,2]时,f(x)max=2,f(x)min=-2. 则对于区间[-2,2]上任意两个自变量的值x1,x2,都有 所以c的最小值为4 8分 (3)∵点M(2,m)(m≠2)不在曲线y=f(x)上,∴设切点为(x0,y0).则 则 因为过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线, 所以方程 即函数g(x)=2x3-6x2+6+m有三个不同的零点. 则
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


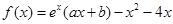 ,曲线
,曲线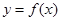 在点
在点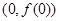 处切线方程为
处切线方程为 .
.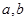 的值;
的值;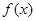 的单调性,并求
的单调性,并求 ,在点
,在点 处的切线方程为
处的切线方程为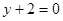 .
. 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有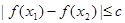 ,求实数
,求实数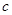 的最小值;
的最小值; ,可作曲线
,可作曲线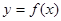 的三条切线,求实数
的三条切线,求实数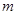 的取值范围.
的取值范围.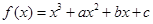 ,曲线
,曲线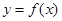 在点
在点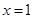 处的切线为
处的切线为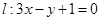 ,若
,若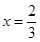 时,
时,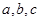 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.