题目内容
已知函数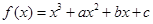 ,曲线
,曲线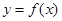 在点
在点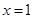 处的切线为
处的切线为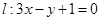 ,若
,若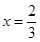 时,
时,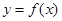 有极值.
有极值.
(1)求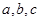 的值;
的值;
(2)求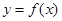 在
在 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1) ;
;
(2)y=f(x)在[-3,1]上的最大值为13,最小值为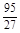
【解析】第一问中利用曲线 在点
在点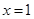 处的切线为
处的切线为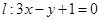 ,若
,若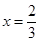 时,
时, 有极值.
有极值.
得到关于参数a,b,c的关系式,求解得到结论。
第二问中 ,在第一问的基础上,进一步求导数,利用导数的正负判定函数的单调性,并求解在给定区间的极值,然后比较极值和端点值的大小关系得到最值。
解:(1)由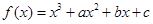 得,
得,
当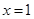 时,切线
时,切线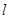 的斜率为3,可得
的斜率为3,可得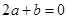 ①
①
当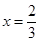 时,
时, 有极值,得
有极值,得
可得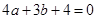 ②
②
由①②解得
由于切点的横坐标为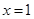 ∴
∴
∴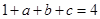
∴
(2)由(1)可得
∴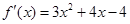
令 ,得
,得 ,
,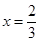
当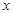 变化时,
变化时,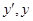 的取值及变化如下表:
的取值及变化如下表:
真确列出表得
|
|
|
|
|
|
|
|
1 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
13 |
|
|
|
4 |
∴ y=f(x)在[-3,1]上的最大值为13,最小值为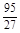

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



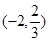


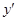
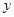





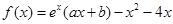 ,曲线
,曲线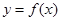 在点
在点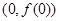 处切线方程为
处切线方程为 .
.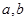 的值;
的值;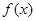 的单调性,并求
的单调性,并求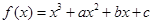 ,曲线
,曲线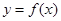 在点
在点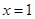 处的切线为
处的切线为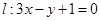 ,若
,若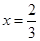 时,
时, 的值;
的值;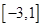 上的最大值和最小值.
上的最大值和最小值.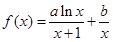 ,曲线
,曲线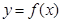 在点
在点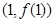 处的切线方程为
处的切线方程为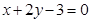 。
。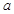 、
、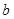 的值;
的值;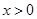 ,且
,且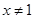 时,
时,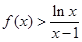 .
.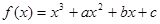 ,曲线
,曲线 在点
在点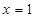 处的切线为
处的切线为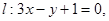 若
若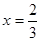 时,
时,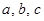 的值;
的值;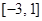 上的最大值和最小值.
上的最大值和最小值.