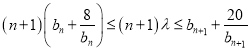Question

【题目】已知数列,为其前n项的和，满足.

(1)求数列的通项公式；

(2)设数列的前n项和为，数列的前n项和为，求证:当时；

(3)若函数的定义域为R，并且，求证.

Answer 1

【答案】(1)；(2)见解析；(3)见解析.

【解析】

(1)当时，,当.

(2)求出数列的通项公式可后求前n项和及，整理得，也可用数学归纳法证明该等式.

(3)结合函数的定义域及已知极限可得，再就的符号分类讨论可证.

解:(1)当时，，

当时,，

∴.

(2)法一：∵，∴，

∴

.

法二：数学归纳法.

①时，,，等式成立.

②假设时有，

当时，，

又

.

故即，

∴是原式也成立，

由①②可知当时.

(3) ∵函数的定义域为，所以恒不为零，

而的值域为，∴.

又时，，与矛盾，故.

易知，否则若，则，与矛盾，

若，则，与矛盾，

∴，∴即有.