题目内容
【题目】在平面直角坐标系中,已知点![]() ,点
,点![]() 在直线
在直线![]() 上运动,过点
上运动,过点![]() 与
与![]() 垂直的直线和线段
垂直的直线和线段![]() 的垂直平分线相交于点
的垂直平分线相交于点![]() 。
。
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过(1)中轨迹![]() 上的点
上的点![]() 作两条直线分别与轨迹
作两条直线分别与轨迹![]() 相交于
相交于![]() ,
,![]() 两点。试探究:当直线
两点。试探究:当直线![]() 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线![]() 的斜率是否为定值?若是,求出这个定值;若不是,说明理由。
的斜率是否为定值?若是,求出这个定值;若不是,说明理由。
【答案】(1)![]() ;(2) 直线
;(2) 直线![]() 的斜率为定值
的斜率为定值![]() .
.
【解析】
试题分析:(1)由![]() 得点
得点![]() 的轨迹符合抛物线的定义,可求出点
的轨迹符合抛物线的定义,可求出点![]() 的轨迹方程;
的轨迹方程;
(2) ![]() 在抛物线
在抛物线![]() 上,则
上,则 作差得
作差得![]() ,直线
,直线![]() 方程为
方程为![]() ,与抛物线方程联立得
,与抛物线方程联立得![]() ,所以有
,所以有![]() ,即
,即![]() ,同理得
,同理得![]() ,代入
,代入![]() 计算即可.
计算即可.
试题解析: (1)依题意,![]() ,故动点
,故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,∴动点
为准线的抛物线,∴动点![]() 的轨迹
的轨迹![]() 为
为![]()
(2)∵![]() 在抛物线
在抛物线![]() 上,∴
上,∴
由①-②可得,![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ……③
……③
设直线![]() 方程为
方程为![]() ,由
,由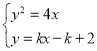 得
得![]()
由![]() ,于是
,于是![]() ,同理可得
,同理可得![]()
∴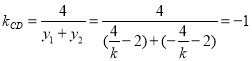 ∴直线
∴直线![]() 的斜率为定值
的斜率为定值![]() 。
。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目

