题目内容
(本小题满分15分) 如图,在三棱锥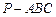 中,
中, ,
, ,点
,点 分别是
分别是 的中点,
的中点, 底面
底面 .
.
(1)求证: 平面
平面 ;
;
(2)当 时,求直线
时,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)当 为何值时,
为何值时,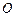 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心.
的重心.
 中,
中, ,
, ,点
,点 分别是
分别是 的中点,
的中点, 底面
底面 .
.(1)求证:
 平面
平面 ;
;(2)当
 时,求直线
时,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)当
 为何值时,
为何值时,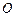 在平面
在平面 内的射影恰好为
内的射影恰好为 的重心.
的重心.
(1)证明见解析。
(2)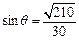
(3)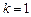
(2)
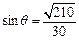
(3)
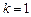
(1)证明: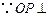 平面
平面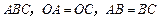 ,
,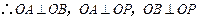 .
.
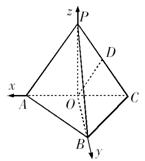
以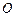 为原点,建立如图所示空间直角坐标系
为原点,建立如图所示空间直角坐标系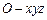 .
.
设 ,则
,则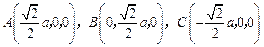 .
.
设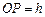 ,则
,则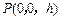 .
.
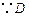 为
为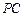 的中点,
的中点, .
.
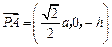 ,
,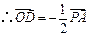 .
.
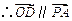 ,
,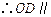 平面
平面 .
.
(2) ,即
,即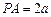 ,
,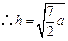 ,
,
可求得平面 的法向量
的法向量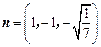 .
.
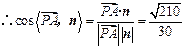 .
.
设 与平面
与平面 所成的角为
所成的角为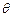 ,
,
则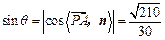 .
.
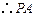 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为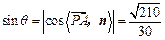 .
.
(3) 的重心
的重心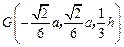 ,
,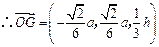 ,
, 平面
平面 ,
,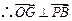 .又
.又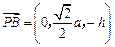 ,
,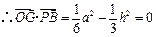 .
.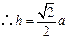 .
.
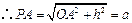 ,即
,即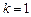 .反之,当
.反之,当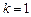 时,三棱锥
时,三棱锥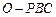 为正三棱锥.
为正三棱锥.
 在平面
在平面 内的射影为
内的射影为 的重心.
的重心.
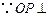 平面
平面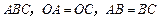 ,
,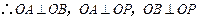 .
.以
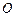 为原点,建立如图所示空间直角坐标系
为原点,建立如图所示空间直角坐标系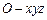 .
.
设
 ,则
,则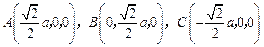 .
.设
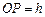 ,则
,则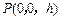 .
.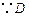 为
为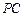 的中点,
的中点, .
.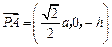 ,
,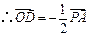 .
.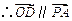 ,
,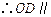 平面
平面 .
.(2)
 ,即
,即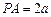 ,
,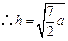 ,
,
可求得平面
 的法向量
的法向量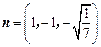 .
.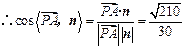 .
.设
 与平面
与平面 所成的角为
所成的角为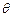 ,
,则
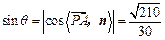 .
.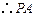 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为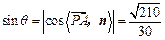 .
.(3)
 的重心
的重心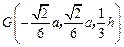 ,
,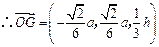 ,
, 平面
平面 ,
,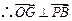 .又
.又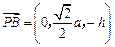 ,
,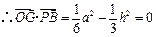 .
.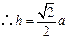 .
.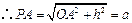 ,即
,即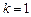 .反之,当
.反之,当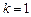 时,三棱锥
时,三棱锥 为正三棱锥.
为正三棱锥. 在平面
在平面 内的射影为
内的射影为 的重心.
的重心.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 CD=1,PD=
CD=1,PD= .
.
 ?
? 的底面为直角梯形,
的底面为直角梯形, ,
,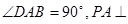 底面
底面 ,且
,且 ,
, ,
, 是
是 的中点。
的中点。 面
面 ;
; 与
与 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.
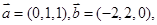 ,则向量
,则向量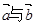 的夹角为
的夹角为



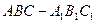 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ,侧棱
,侧棱 ,D,E分别是
,D,E分别是 与
与 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是 的重心G.则
的重心G.则
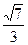


 中,
中, ,
, 面
面 ,
, ,求面
,求面 与面
与面 所成二面角的正切值.
所成二面角的正切值. ,且l的方向向量为(2, m, 1), 平面
,且l的方向向量为(2, m, 1), 平面 , 2), 则m= .
, 2), 则m= .