题目内容
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]()
![]() ,使得函数
,使得函数![]() 同时满足:
同时满足:
(1)![]() 在
在![]() 内是单调函数;
内是单调函数;
(2)![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的“
的“![]() 倍值区间”.
倍值区间”.
下列函数中存在“3倍值区间”的有_____.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
【答案】①③
【解析】对于①,若函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() ,则有
,则有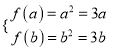 ,解得
,解得![]() .所以函数函数
.所以函数函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() .
.
对于②,若函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() ,则有
,则有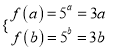 ,结合图象可得方程
,结合图象可得方程![]() 无解.所以函数函数
无解.所以函数函数![]() 不存在“3倍值区间”.
不存在“3倍值区间”.
对于③,当![]() 时,
时, ![]() .当
.当![]() 时,
时,  ,从而可得函数
,从而可得函数![]() 在区间
在区间![]() 上单调递增.若函数
上单调递增.若函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() ,且
,且![]()
![]()
![]() ,则有
,则有 ,解得
,解得![]() .所以函数
.所以函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() .
.
对于④,函数![]() 为增函数,若函数
为增函数,若函数![]() 存在“3倍值区间”
存在“3倍值区间” ![]() ,则
,则
 ,由图象可得方程
,由图象可得方程![]() 无解,故函数
无解,故函数![]() 不存在“3倍值区间”.
不存在“3倍值区间”.
综上可得①③正确.
答案:①③

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下: 表1:男生表2:女生
等级 | 优秀 | 合格 | 尚待改进 | 等级 | 优秀 | 合格 | 尚待改进 | |
频数 | 15 | x | 5 | 频数 | 15 | 3 | y |
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考数据与公式:
K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2>k0) | 0.05 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |

