题目内容
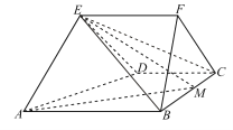
【题目】如图所示的五面体![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,
, ![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 为线段
为线段![]() 上的动点,求证:
上的动点,求证:![]() 与
与![]() 不垂直.
不垂直.
【答案】(I)![]() (II)见解析(III)见解析
(II)见解析(III)见解析
【解析】
(Ⅰ)取AD中点N,连接EN.可得EN⊥AD.由平面ADE⊥平面ABCD,利用面面垂直的性质可得EN⊥平面ABCD.再由已知求得梯形ABCD得面积,代入棱锥体积公式求解;(Ⅱ)由AB∥CD,得CD∥平面ABFE.进一步得到CD∥EF.再由线面平行的判定可得EF∥平面ABCD;(Ⅲ)连接MN,假设EM⊥AM.结合(Ⅰ)利用反证法证明EM与AM不垂直.
(Ⅰ)取AD中点![]() ,连接
,连接![]() .
.

在![]() 中,
中,![]() ,
,
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面ADE,
平面ADE,
所以![]() 平面
平面![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() .
.
(Ⅱ)因为![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(Ⅲ)连接![]() ,假设
,假设![]() .
.
由(Ⅰ)知![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() , 且
, 且![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
在△![]() 中,
中,![]() ,
,
所以![]() .
.
所以![]() .
.
这与![]() 矛盾.
矛盾.
所以假设不成立,即![]() 与
与![]() 不垂直.
不垂直.

 ABC考王全优卷系列答案
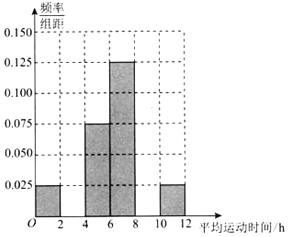
ABC考王全优卷系列答案【题目】已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:h),汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:
平均运动时间 | 频数 | 频率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合计 | 300 | 1 |
(1)求抽取的女职工的人数;
(2)①根据频率分布表,求出m、n、p的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h的概率;
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下2×2列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |