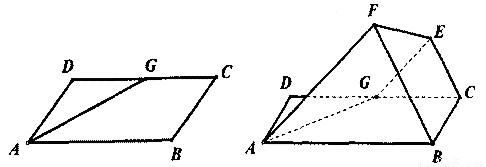
题目内容
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.(I)求证:平面ABFCE∥平面CGE;
(II)若平面AGEF⊥平面ABCD,求二面B-EF-A的平面角的余弦值.

【答案】分析:(I)证明AF∥平面CGE,AB∥平面CGE,即可证明平面ABFCE∥平面CGE;
(II)FG⊥平面ABCD,BG⊥平面AGEF,作GH⊥EF交EF于H,连BH,则BH⊥EF,从而可知∠BHG为二面B-EF-A的平面角,即可求得二面角B-EF-A的平面角的余弦值.
解答: (I)证明:∵AB∥CG,GE∥AF,
(I)证明:∵AB∥CG,GE∥AF,
∴AF∥平面CGE,AB∥平面CGE
∵AF∩AB=A
∴平面ABFCE∥平面CGE;
(II)解:∠BAD=60°,AB=6,AD=3,G为CD中点
∴BG⊥AG,∴FG⊥AG
∵平面AGEF⊥平面ABCD,FG?平面AGEF
∴FG⊥平面ABCD,
∵BG?平面ABCD
∴FG⊥BG
∵AG∩FG=G
∴BG⊥平面AGEF
作GH⊥EF交EF于H,连BH,则BH⊥EF
∴∠BHG为二面B-EF-A的平面角
∵BG=3,GH= ,∴
,∴
∴
∴二面角-EF-A的平面角的余弦值为 .
.
点评:本题考查面面平行,考查面面角,解题的关键是熟练掌握面面平行的判定,正确作出面面角.
(II)FG⊥平面ABCD,BG⊥平面AGEF,作GH⊥EF交EF于H,连BH,则BH⊥EF,从而可知∠BHG为二面B-EF-A的平面角,即可求得二面角B-EF-A的平面角的余弦值.
解答:
 (I)证明:∵AB∥CG,GE∥AF,
(I)证明:∵AB∥CG,GE∥AF,∴AF∥平面CGE,AB∥平面CGE
∵AF∩AB=A
∴平面ABFCE∥平面CGE;
(II)解:∠BAD=60°,AB=6,AD=3,G为CD中点
∴BG⊥AG,∴FG⊥AG
∵平面AGEF⊥平面ABCD,FG?平面AGEF
∴FG⊥平面ABCD,
∵BG?平面ABCD
∴FG⊥BG
∵AG∩FG=G
∴BG⊥平面AGEF
作GH⊥EF交EF于H,连BH,则BH⊥EF
∴∠BHG为二面B-EF-A的平面角
∵BG=3,GH=
 ,∴
,∴
∴

∴二面角-EF-A的平面角的余弦值为
 .
.点评:本题考查面面平行,考查面面角,解题的关键是熟练掌握面面平行的判定,正确作出面面角.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
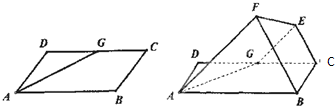 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.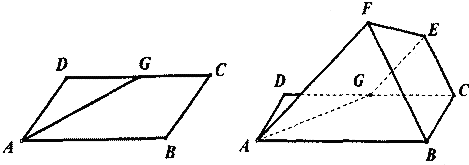 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG. 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.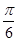 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD