题目内容
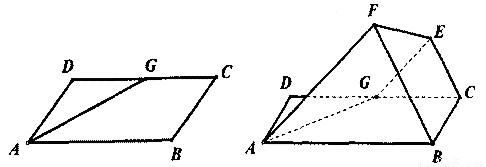
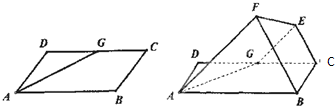 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.(1)求证:直线CE∥平面ABF;
(2)如果FG⊥平面ABCD求二面B-EF-A的平面角的余弦值.
分析:(1)要证直线CE∥平面ABF,只要证明CE所在的平面CEG平行于平面ABF即可,由已知条件利用面面平行的判定进行证明;
(2)利用已知条件结合余弦定理证明AG⊥BG,再由FG⊥平面ABCD,可以GA、GB、GF为坐标轴建立如图空间直角坐标系,然后找到所用点的坐标,分别求出二面角的两个半平面的一个法向量,利用平面法向量求二面角的平面角的余弦值.
(2)利用已知条件结合余弦定理证明AG⊥BG,再由FG⊥平面ABCD,可以GA、GB、GF为坐标轴建立如图空间直角坐标系,然后找到所用点的坐标,分别求出二面角的两个半平面的一个法向量,利用平面法向量求二面角的平面角的余弦值.
解答: (1)证明:如图,∵ABCD是平行四边形,
(1)证明:如图,∵ABCD是平行四边形,
∴CG∥AB,∴CG∥平面ABF,GE∥AF,
∴GE∥平面ABF,∵GE∩GC=G,∴平面CEG∥平面ABF.
∴CE∥平面ABF;
(2)解:∵∠BAD=60°,AB=6,AD=3,G为CD中点,∴BG=GC=BC=3,
由余弦定理AG2=AD2+GD2-2AD•GD•COS120°=27,
∴AG2+BG2=AB2,∴AG⊥BG
又FG⊥平面ABCD,
∴以GA、GB、GF为坐标轴建立如图空间直角坐标系,则
A(3
,0,0),B(0,3,0),F(0,0,3),C(-
,
,0)
∴平面AEF的法向量
=
=(0,3,0),
=(-
,-
,0),
=(0,-3,3)
设平面BFEC的法向量为
=
=(x,y,z),则
,∴
令y=1,则x=-
,z=1,∴
=(-
,1,1)
∴cosθ=|cos<
,
>|=|
|=|
|=
即为所求.
 (1)证明:如图,∵ABCD是平行四边形,
(1)证明:如图,∵ABCD是平行四边形,∴CG∥AB,∴CG∥平面ABF,GE∥AF,
∴GE∥平面ABF,∵GE∩GC=G,∴平面CEG∥平面ABF.
∴CE∥平面ABF;
(2)解:∵∠BAD=60°,AB=6,AD=3,G为CD中点,∴BG=GC=BC=3,
由余弦定理AG2=AD2+GD2-2AD•GD•COS120°=27,
∴AG2+BG2=AB2,∴AG⊥BG
又FG⊥平面ABCD,
∴以GA、GB、GF为坐标轴建立如图空间直角坐标系,则
A(3
| 3 |
3
| ||
| 2 |
| 3 |
| 2 |
∴平面AEF的法向量
| n1 |
| GB |
| BC |
3
| ||
| 2 |
| 3 |
| 2 |
| BF |
设平面BFEC的法向量为
| n2 |
| n |
|
|
令y=1,则x=-
| ||
| 3 |
| n |
| ||
| 3 |
∴cosθ=|cos<
| n1 |
| n2 |
| ||||
|
|
| 3 | ||||||
3×
|
| ||
| 7 |
点评:本题考查了直线与平面平行的判定,考查了利用空间向量求二面角的大小,解答的关键是建立正确的空间右手系,是中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
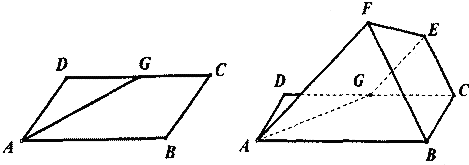 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG. 如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.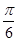 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD