题目内容
已知函数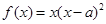 ,
,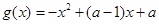 (其中
(其中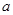 为常数);
为常数);
(Ⅰ)如果函数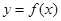 和
和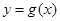 有相同的极值点,求
有相同的极值点,求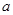 的值;
的值;
(Ⅱ)设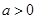 ,问是否存在
,问是否存在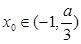 ,使得
,使得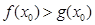 ,若存在,请求出实数
,若存在,请求出实数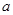 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅲ)记函数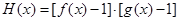 ,若函数
,若函数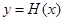 有5个不同的零点,求实数
有5个不同的零点,求实数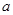 的取值范围.
的取值范围.
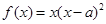 ,
,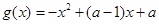 (其中
(其中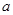 为常数);
为常数);(Ⅰ)如果函数
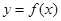 和
和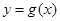 有相同的极值点,求
有相同的极值点,求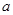 的值;
的值;(Ⅱ)设
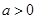 ,问是否存在
,问是否存在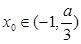 ,使得
,使得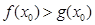 ,若存在,请求出实数
,若存在,请求出实数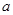 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(Ⅲ)记函数
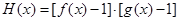 ,若函数
,若函数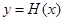 有5个不同的零点,求实数
有5个不同的零点,求实数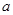 的取值范围.
的取值范围.(Ⅰ)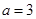 或
或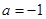 (Ⅱ)
(Ⅱ)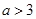 (Ⅲ)
(Ⅲ)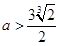
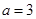 或
或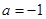 (Ⅱ)
(Ⅱ)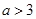 (Ⅲ)
(Ⅲ)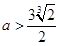
试题分析:(1)对函数f(x)求导可得
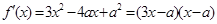 ,由
,由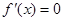 ,可得得
,可得得 或
或 ,而
,而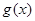 在
在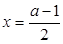 处有极大值,从而可得a;(2)假设存在,即存在x∈(?1,
处有极大值,从而可得a;(2)假设存在,即存在x∈(?1, ),使得f(x)-g(x)>0,由x∈(?1,
),使得f(x)-g(x)>0,由x∈(?1, ),及a>0,可得x-a<0,则存在x∈(?1,
),及a>0,可得x-a<0,则存在x∈(?1, ),使得
),使得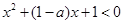 ,结合二次函数的性质求解;(3)据题意有f(x)-1=0有3个不同的实根,g(x)-1=0有2个不同的实根,且这5个实根两两不相等.g(x)-1=0有2个不同的实根,只需满足
,结合二次函数的性质求解;(3)据题意有f(x)-1=0有3个不同的实根,g(x)-1=0有2个不同的实根,且这5个实根两两不相等.g(x)-1=0有2个不同的实根,只需满足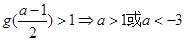 ⇒a>1或a<?3;
⇒a>1或a<?3;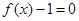 有3个不同的实根,从而结合导数进行求解.
有3个不同的实根,从而结合导数进行求解.试题解析:(Ⅰ)
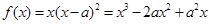 ,则
,则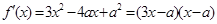 ,
,令
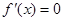 ,得
,得 或
或 ,而
,而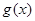 在
在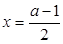 处有极大值,∴
处有极大值,∴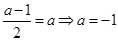 ,或
,或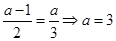 ;综上:
;综上: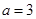 或
或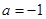 . (3分)
. (3分)(Ⅱ)假设存在,即存在
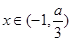 ,使得
,使得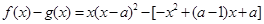
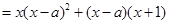
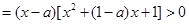 ,
,当
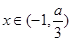 时,又
时,又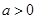 ,故
,故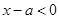 ,则存在
,则存在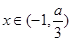 ,使得
,使得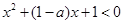 , (4分)
, (4分)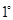 当
当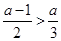 即
即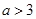 时,
时,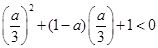 得
得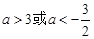 ,
,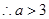 ; (5分)
; (5分)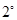 当
当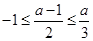 即
即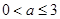 时,
时,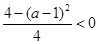 得
得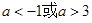 , (6分)
, (6分)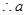 无解;综上:
无解;综上: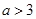 . (7分)
. (7分)(Ⅲ)据题意有
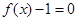 有3个不同的实根,
有3个不同的实根,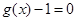 有2个不同的实根,且这5个实根两两不相等.
有2个不同的实根,且这5个实根两两不相等.(ⅰ)
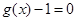 有2个不同的实根,只需满足
有2个不同的实根,只需满足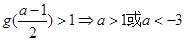 ; (8分)
; (8分)(ⅱ)
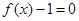 有3个不同的实根,
有3个不同的实根,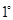 当
当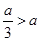 即
即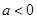 时,
时,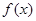 在
在 处取得极大值,而
处取得极大值,而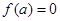 ,不符合题意,舍; (9分)
,不符合题意,舍; (9分)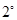 当
当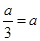 即
即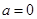 时,不符合题意,舍;
时,不符合题意,舍;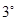 当
当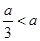 即
即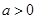 时,
时,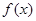 在
在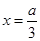 处取得极大值,
处取得极大值,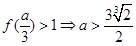 ;所以
;所以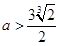 ; (10分)
; (10分)因为(ⅰ)(ⅱ)要同时满足,故
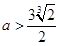 ;(注:
;(注: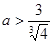 也对) (11分)
也对) (11分)下证:这5个实根两两不相等,即证:不存在
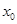 使得
使得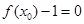 和
和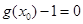 同时成立;
同时成立;若存在
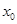 使得
使得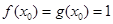 ,
,由
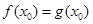 ,即
,即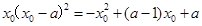 ,得
,得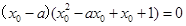 ,
,当
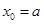 时,
时,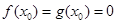 ,不符合,舍去;
,不符合,舍去;当
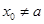 时,既有
时,既有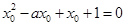 ①;
①;又由
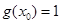 ,即
,即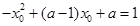 ②; 联立①②式,可得
②; 联立①②式,可得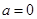 ;
;而当
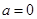 时,
时,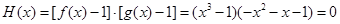 没有5个不同的零点,故舍去,所以这5个实根两两不相等.
没有5个不同的零点,故舍去,所以这5个实根两两不相等.综上,当
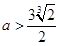 时,函数
时,函数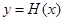 有5个不同的零点. (14分)
有5个不同的零点. (14分)
练习册系列答案
相关题目
 ,
, .
. ,求函数
,求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数 满足
满足 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: .
.
 时,求
时,求 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ;
;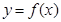 在
在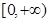 上单调递增;
上单调递增;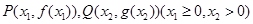 ,若直线PQ∥x轴,求P,Q两点间的最短距离.
,若直线PQ∥x轴,求P,Q两点间的最短距离.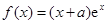 ,其中
,其中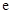 是自然对数的底数,
是自然对数的底数,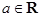 .
.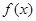 的单调区间;
的单调区间;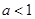 时,试确定函数
时,试确定函数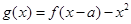 的零点个数,并说明理由.
的零点个数,并说明理由.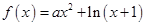 .
.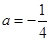 时,求函数
时,求函数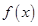 的单调区间;
的单调区间;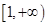 上为减函数,求实数
上为减函数,求实数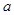 的取值范围;
的取值范围;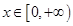 时,不等式
时,不等式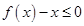 恒成立,求实数
恒成立,求实数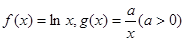 ,设
,设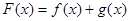
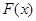 的单调区间
的单调区间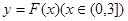 图象上任意一点
图象上任意一点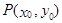 为切点的切线的斜率
为切点的切线的斜率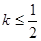 恒成立,求实数
恒成立,求实数 的最小值
的最小值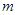 ,使得函数
,使得函数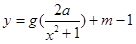 的图象与函数
的图象与函数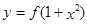 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数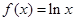 ,
,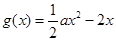 .
.
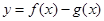 在
在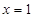 与
与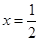 处的切线相互平行,求
处的切线相互平行,求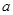 的值及切线斜率;
的值及切线斜率;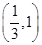 上单调递减,求
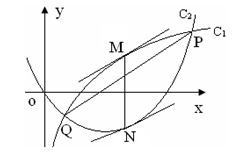
上单调递减,求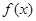 的图像C1与函数
的图像C1与函数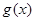 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行. 的值域为 .
的值域为 .