题目内容
1．某车间计划全年完成产值60万元，前3个季度完成43.45万元，如果10月份的产值是5万元，那么后两个月的月平均增长率应该是多少，才能超额完成年产值计划？分析 通过设后两个月的月平均增长率为x，进而解不等式5+5（1+x）+5（1-x）2+43.45＞60即得结论．
解答 解：设后两个月的月平均增长率为x，
则5+5（1+x）+5（1-x）2+43.45＞60，
整理得：x2+3x-0.31＞0，
解得：x＞0.1或x＜-3.1（舍），
答：后两个月的月平均增长率在10%以上才能超额完成年产值计划．
点评 本题是一道关于一元二次不等式的简单应用题，考查分析问题、解决问题的能力，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
11．
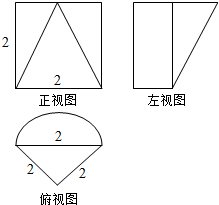正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体，该几何体的三视图如图所示，则该几何体的表面积为（ ）
正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体，该几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | 3π+4+$\sqrt{3}$+$\sqrt{7}$ | B． | 3π+6+$\sqrt{3}$ | C． | 2π+4+$\sqrt{3}$$+\sqrt{7}$ | D． | 2π+6$+\sqrt{3}$ |
9．双曲线C；$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0））的左右焦点分别为F1，F2，双曲线C上一点P到右焦点F2的距离是实轴两端点到右焦点距离的等差中项，若△PF1F2为锐角三角形，则双曲线C的离心率的取值范围是（ ）
| A． | （$\frac{1+\sqrt{5}}{2}$，+∞） | B． | （1，1+$\sqrt{3}$） | C． | （$\frac{1+\sqrt{5}}{2}$，1+$\sqrt{3}$） | D． | （$\frac{1+\sqrt{5}}{2}$，2）∪（2，1+$\sqrt{3}$） |
如图，点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，过点F的直线的斜率为3，与双曲线交于P，Q两点，分别过P、Q向右准线作垂线，垂足分别为M，N，且$\overrightarrow{PM}$=3$\overrightarrow{QN}$，求双曲线的离心率的大小．
10．已知$\overrightarrow{a}$=（5，6），$\overrightarrow{b}$=（sinα，cosα），已知向量且$\overrightarrow{a}$∥$\overrightarrow{b}$，则tanα=（ ）
| A． | $\frac{5}{6}$ | B． | -$\frac{5}{6}$ | C． | $\frac{6}{5}$ | D． | -$\frac{6}{5}$ |