题目内容
5.已知函数$f(x)=\left\{\begin{array}{l}cx+1(0<x<c)\\{2^{-\frac{x}{c^2}}}+1(c≤x<1)\end{array}\right.$满足$f({c^2})=\frac{9}{8}$,则常数c的值是$\frac{1}{2}$.分析 由已知条件利用分段函数的性质,能求出常数c的值.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}cx+1(0<x<c)\\{2^{-\frac{x}{c^2}}}+1(c≤x<1)\end{array}\right.$满足$f({c^2})=\frac{9}{8}$,
∴当0<c2<1时,f(c2)=c•c2+1=$\frac{9}{8}$,解得c=$\frac{1}{2}$,成立;
当c≤c2<1时,f(c2)=${2}^{-\frac{{c}^{2}}{{c}^{2}}}+1$=$\frac{9}{8}$,不成立.
∴c=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数式中常数c的值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
13.函数f(x)=(x-1)ln|x|的图象大致为( )
| A. |  | B. | 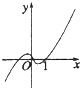 | C. | 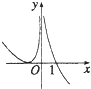 | D. | 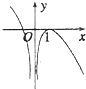 |