题目内容
20．与函数y=2x2-2x+1关于y=-1对称的函数解析式为：y=-2x2+2x-2．分析 将原函数的图象向上平移1个单位，然后作关于x轴的对称图象，再将所得图象向下平移1个单位，这时所得图象的函数解析式即为所求函数解析式，函数沿y轴方向平移及函数关于x轴的对称函数解析式是可以求出的，从而可得到原函数关于直线y=-1对称的函数解析式．
解答 解：可这样考虑：将原函数的图象向上平移1个单位，然后作关于x轴的对称图象，再将所得对称图象向下平移1个单位，即得到原函数关于y=-1的对称图象；
原函数向上平移1个单位得到，y=2x2-2x+2，该函数关于x轴的对称函数为y=-2x2+2x-1，该函数向下平移1个单位得到y=-2x2+2x-1-1；
∴与函数y=2x2-2x+1关于y=-1对称的函数解析式为：y=-2x2+2x-2．
故答案为：y=-2x2+2x-2．
点评 考查曲线关于直线对称的概念，应知道f（x）和-f（x）关于直线y=0，即x轴对称，掌握函数沿y轴方向平移的过程．
练习册系列答案
相关题目
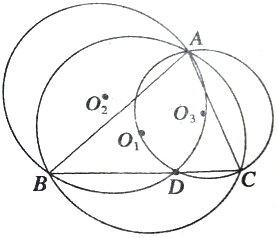如图，D是△ABC的BC边上的一点，O1，O2和O3分别为△ABC，△ADB和△ADC外接圆的圆心，求证：A，O2，O1，O3四点共圆．