题目内容
(本小题满分16分)已知常数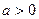 ,函数
,函数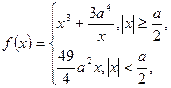
(1)求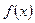 的单调递增区间;
的单调递增区间;
(2)若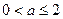 ,求
,求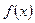 在区间
在区间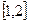 上的最小值
上的最小值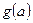 ;
;
(3)是否存在常数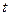 ,使对于任意
,使对于任意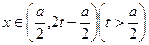 时,
时,
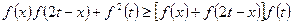 恒成立,若存在,求出
恒成立,若存在,求出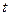 的值;若不存在,说明理由。
的值;若不存在,说明理由。
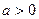 ,函数
,函数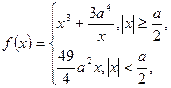
(1)求
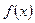 的单调递增区间;
的单调递增区间;(2)若
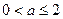 ,求
,求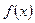 在区间
在区间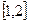 上的最小值
上的最小值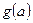 ;
;(3)是否存在常数
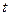 ,使对于任意
,使对于任意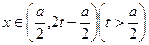 时,
时,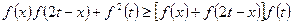 恒成立,若存在,求出
恒成立,若存在,求出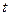 的值;若不存在,说明理由。
的值;若不存在,说明理由。⑴当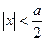 时,
时,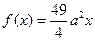 为增函数. …………………………………(1分)
为增函数. …………………………………(1分)
当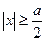 时,
时,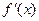 =
=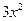
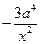 .令
.令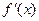
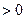 ,得
,得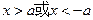 .…………(3分)
.…………(3分)
∴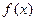 的增区间为
的增区间为 ,
,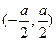 和
和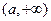 .……………………………(4分)
.……………………………(4分)
⑵由图可知,
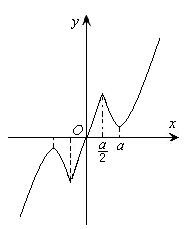
①当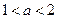 时,
时,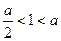 ,
,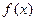 在区间
在区间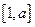 上递减,在
上递减,在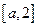 上递增,最小值为
上递增,最小值为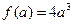 ;………(6分)
;………(6分)
②当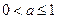 时,
时,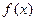 在区间
在区间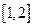 为增函数,最小值为
为增函数,最小值为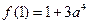 ;……………………………(8分)
;……………………………(8分)
③当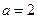 时,
时,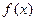 在区间
在区间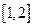 为增函数,最小值为
为增函数,最小值为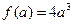 ;……………………………(9分)
;……………………………(9分)
综上,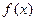 最小值
最小值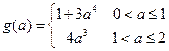 . ………………………………(10分)
. ………………………………(10分)
⑶由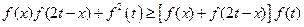 ,
,
可得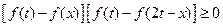 , ………………………………(12分)
, ………………………………(12分)
即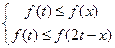 或
或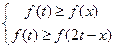 成立,所以
成立,所以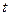 为极小值点,或
为极小值点,或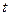 为极大值点.又
为极大值点.又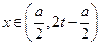 时
时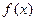 没有极大值,所以
没有极大值,所以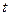 为极小值点,即
为极小值点,即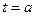 ……………(16分)
……………(16分)
(若只给出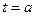 ,不说明理由,得1分)
,不说明理由,得1分)
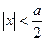 时,
时,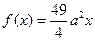 为增函数. …………………………………(1分)
为增函数. …………………………………(1分)当
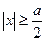 时,
时,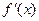 =
=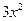
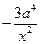 .令
.令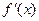
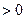 ,得
,得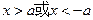 .…………(3分)
.…………(3分)∴
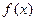 的增区间为
的增区间为 ,
,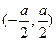 和
和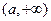 .……………………………(4分)
.……………………………(4分)⑵由图可知,

①当
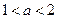 时,
时,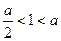 ,
,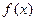 在区间
在区间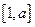 上递减,在
上递减,在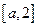 上递增,最小值为
上递增,最小值为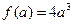 ;………(6分)
;………(6分) ②当
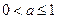 时,
时,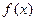 在区间
在区间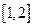 为增函数,最小值为
为增函数,最小值为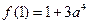 ;……………………………(8分)
;……………………………(8分)③当
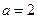 时,
时,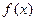 在区间
在区间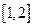 为增函数,最小值为
为增函数,最小值为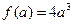 ;……………………………(9分)
;……………………………(9分)综上,
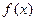 最小值
最小值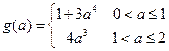 . ………………………………(10分)
. ………………………………(10分)⑶由
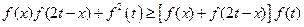 ,
,可得
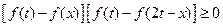 , ………………………………(12分)
, ………………………………(12分)即
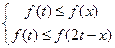 或
或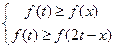 成立,所以
成立,所以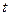 为极小值点,或
为极小值点,或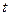 为极大值点.又
为极大值点.又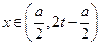 时
时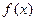 没有极大值,所以
没有极大值,所以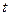 为极小值点,即
为极小值点,即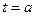 ……………(16分)
……………(16分) (若只给出
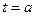 ,不说明理由,得1分)
,不说明理由,得1分)略

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 是
是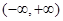 上的减函数,那么
上的减函数,那么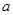 的取值范围是
的取值范围是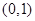



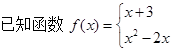

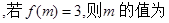 ( )
( ) 满足:当
满足:当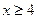 时,
时,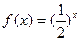 ,当
,当 时,
时,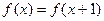 ,那么
,那么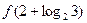 等于( )
等于( )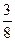

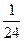
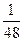
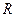 的函数
的函数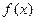 在
在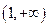 上为减函数,且函数
上为减函数,且函数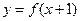 为偶函数,则( )
为偶函数,则( )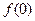 >
>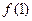
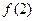
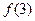
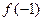 <
<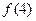
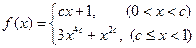 ,若
,若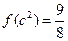 ,则不等式
,则不等式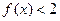 的解集为
的解集为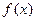 是定义在R上的函数,对
是定义在R上的函数,对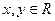 都有
都有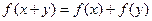 ,且当
,且当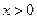 时,
时,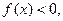
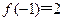 。
。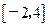 上的最值。
上的最值。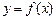 是奇函数,当
是奇函数,当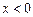 时,
时,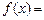
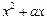
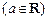 ,且
,且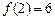 ,则
,则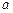 = .
= .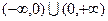 上的奇函数
上的奇函数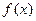 ,在
,在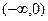 单调递增,且
单调递增,且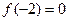 ,则不等式
,则不等式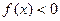 的解集是_________________
的解集是_________________