题目内容
((本小题满分14分)
已知函数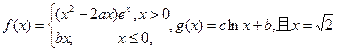 是函数
是函数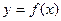 的极值点。
的极值点。
(Ⅰ)当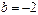 时,求a的值,讨论函数
时,求a的值,讨论函数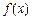 的单调性;
的单调性;
(Ⅱ)当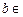 R时,函数
R时,函数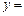
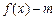 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(Ⅲ)是否存在这样的直线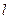 ,同时满足:
,同时满足:
①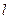 是函数
是函数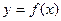 的图象在点
的图象在点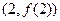 处的切线
处的切线
②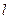
 与函数
与函数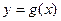 的图象相切于点
的图象相切于点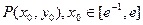 ,
,
如果存在,求实数b的取值范围;不存在,请说明理由。
已知函数
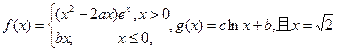 是函数
是函数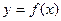 的极值点。
的极值点。(Ⅰ)当
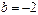 时,求a的值,讨论函数
时,求a的值,讨论函数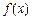 的单调性;
的单调性;(Ⅱ)当
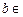 R时,函数
R时,函数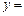
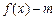 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.(Ⅲ)是否存在这样的直线
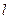 ,同时满足:
,同时满足:①
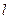 是函数
是函数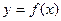 的图象在点
的图象在点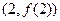 处的切线
处的切线 ②
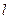
 与函数
与函数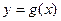 的图象相切于点
的图象相切于点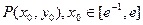 ,
,如果存在,求实数b的取值范围;不存在,请说明理由。
解:(1)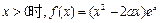 ,
,
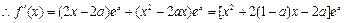 . ....1分
. ....1分
由已知得,
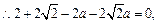 解得a=1. ……2分
解得a=1. ……2分
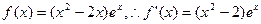 .
.
当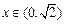 时,
时, ,当
,当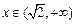 时,
时,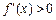 .又
.又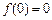 , ....3分
, ....3分
当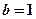 时,
时,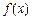 在
在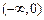 ,
,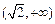 上单调递增,在
上单调递增,在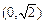 上单调递减. ………4分
上单调递减. ………4分
(2)由(1)知,当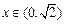 时,
时,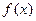 单调递减,
单调递减,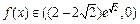
当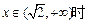 ,
,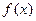 单调递增,
单调递增,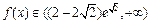 . ………………2分
. ………………2分
要使函数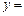
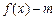 有两个零点,则函数
有两个零点,则函数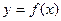 的图象与直线
的图象与直线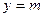 有两个不同的交点.
有两个不同的交点.
①当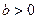 时,m=0或
时,m=0或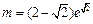 ; ....3分
; ....3分
②当b=0时,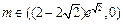 ; ....4分
; ....4分
③当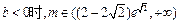 . ..
. .. ..5分
..5分
(3)假设存在,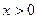 时,
时,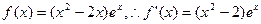
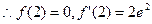
函数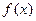 的图象在点
的图象在点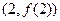 处的切线
处的切线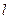 的方程为:
的方程为: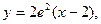 ....1分
....1分
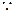 直线
直线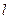 与函数
与函数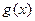 的图象相切于点
的图象相切于点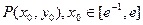 ,
,
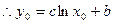 ,
,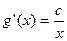 ,所以切线
,所以切线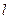 的斜率为
的斜率为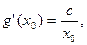
所以切线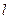 的方程为
的方程为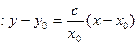
即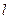 的方程为:
的方程为: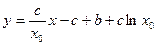 …………2分
…………2分
得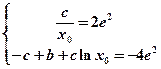
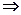
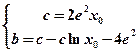
得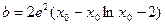 其中
其中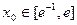 ....3分
....3分
记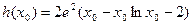 其中
其中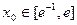
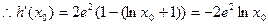
令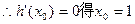 ....4分
....4分
又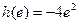 ,
,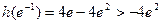
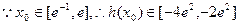
所以实数b的取值范围的集合: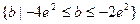 …………5分
…………5分
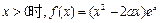 ,
,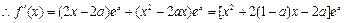 . ....1分
. ....1分由已知得,

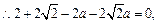 解得a=1. ……2分
解得a=1. ……2分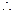
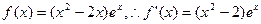 .
.当
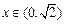 时,
时, ,当
,当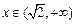 时,
时,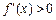 .又
.又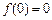 , ....3分
, ....3分当
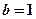 时,
时,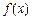 在
在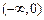 ,
,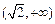 上单调递增,在
上单调递增,在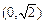 上单调递减. ………4分
上单调递减. ………4分(2)由(1)知,当
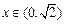 时,
时,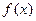 单调递减,
单调递减,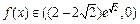
当
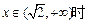 ,
,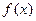 单调递增,
单调递增,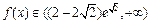 . ………………2分
. ………………2分要使函数
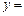
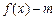 有两个零点,则函数
有两个零点,则函数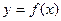 的图象与直线
的图象与直线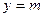 有两个不同的交点.
有两个不同的交点.①当
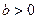 时,m=0或
时,m=0或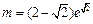 ; ....3分
; ....3分②当b=0时,
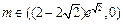 ; ....4分
; ....4分③当
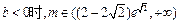 . ..
. .. ..5分
..5分(3)假设存在,
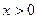 时,
时,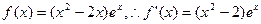
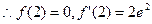
函数
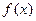 的图象在点
的图象在点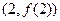 处的切线
处的切线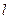 的方程为:
的方程为: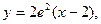 ....1分
....1分 直线
直线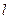 与函数
与函数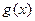 的图象相切于点
的图象相切于点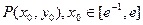 ,
,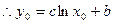 ,
,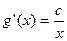 ,所以切线
,所以切线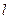 的斜率为
的斜率为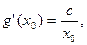
所以切线
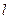 的方程为
的方程为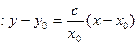
即
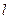 的方程为:
的方程为: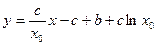 …………2分
…………2分得
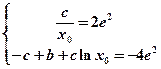
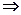
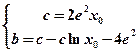
得
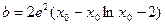 其中
其中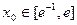 ....3分
....3分记
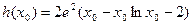 其中
其中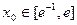
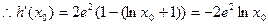
令
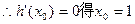 ....4分
....4分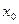 | 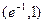 | 1 | 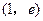 |
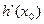 | + | 0 | - |
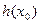 | 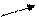 | 极大值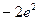 |  |
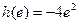 ,
,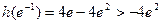
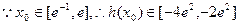
所以实数b的取值范围的集合:
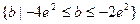 …………5分
…………5分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .
. 的值。
的值。  ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 ,求
,求 (
( 为全集)。
为全集)。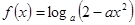 在
在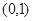 上为减函数,则实数
上为减函数,则实数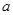 的取值范围
的取值范围

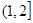

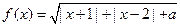 .
.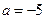 时,求函数
时,求函数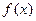 的定义域;
的定义域;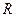 ,试求实数
,试求实数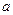 的取值范围.
的取值范围.

 ,销售收入为
,销售收入为 ,写出
,写出 .
. 函数
函数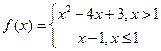 ,则函数
,则函数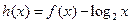 的
的 零点个数为( )
零点个数为( )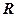 上的函数
上的函数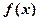 满足:
满足: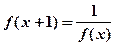 ,当
,当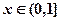 时,
时,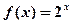 ,则
,则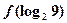 等于__ ▲_ __.
等于__ ▲_ __.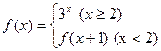 ,则
,则 的值为( )
的值为( )


