题目内容
已知M={(x,y)|y=
,y≠0},N={(x,y)|y=x+b},若M∩N≠∅,则b∈( )
| 9-x2 |
A、[-3
| ||||
B、(-3
| ||||
C、(-3,3
| ||||
D、[-3,3
|
分析:先分析出M中的元素表示的是以(0,0)为圆心,r=3的上半圆,N中的元素是一组平行线上的点,再画出对应图象,知道直线的临界值在相切以及y=x+3之间,求出相切时对应的b即可求得结果.
解答:解:由题得:M中的元素表示的是以(0,0)为圆心,r=3的上半圆,N中的元素是一组平行线上的点.
由M∩N≠∅,得直线与半圆有公共点,画出图形得: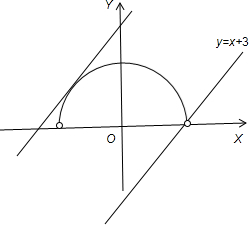
直线的临界值在与圆相切以及y=x+3之间.
相切时,因为(0,0)到直线y=x+b的距离 d=
=3?b=±3
,由图得取b=3
.
所以3<b≤3
.
故选 C.
由M∩N≠∅,得直线与半圆有公共点,画出图形得:

直线的临界值在与圆相切以及y=x+3之间.
相切时,因为(0,0)到直线y=x+b的距离 d=
| |0-0+b| | ||
|
| 2 |
| 2 |
所以3<b≤3
| 2 |
故选 C.
点评:本题主要考查集合和集合之间的运算以及数形结合思想的运用,是对知识点的综合考查,属于基础题.本题的易错点在于没看清题中的限制y≠0,误选答案.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知M={(x,y)|
+
=1},N=(x,y)|y=mx+b,若对于所有的m∈R,均有M∩N≠φ,则b的取值范围是( )
| x2 |
| 3 |
| y2 | ||
|
A、(-∞,-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、[-
|