题目内容
点P是椭圆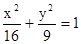 上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
9
解析试题分析:△F1P F2是椭圆的“焦点三角形”。在椭圆中,焦点三角的面积公式是:若椭圆的方程是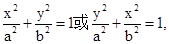 则
则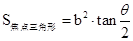 (θ为焦点三角形的顶角)
(θ为焦点三角形的顶角)
所以S=9×tan45°=9,即△F1P F2面积为面积为9.
考点:本题主要考查椭圆的定义、几何性质。
点评:典型题,涉及椭圆的“焦点三角形”问题,一般要利用椭圆的定义。本题利用已有“小结论”,使问题的解决更为方便。

练习册系列答案
相关题目
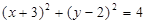 相切的直线方程是___________.
相切的直线方程是___________. 轴上,且过两点
轴上,且过两点 的圆的方程为 .
的圆的方程为 .  (
( 是实数)与圆
是实数)与圆 相交于
相交于 两点,且
两点,且 (
( 是坐标原点)是直角三角形,则点
是坐标原点)是直角三角形,则点 与点
与点 之间距离的最小值是 .
之间距离的最小值是 . 的点数共有______ 个。
的点数共有______ 个。 与圆
与圆 关于直线
关于直线 对称,则
对称,则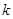 为何实数,直线
为何实数,直线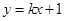 与曲线
与曲线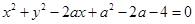 恒有交点,则实数
恒有交点,则实数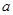 的取值范围为 。
的取值范围为 。 关于
关于 轴对称的圆的方程为______________.
轴对称的圆的方程为______________.  关于直线2x-y+3=0对称的圆的方程是 ___ .
关于直线2x-y+3=0对称的圆的方程是 ___ .