题目内容
过点P(-1,6)且与圆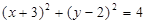 相切的直线方程是___________.
相切的直线方程是___________.
x=-1或3x-4y+27=0
解析试题分析:由题知:圆心O的坐标为(-3,2),半径为2.
当切线斜率不存在时,显然直线x=-1是过P且与圆相切的方程.
当直线斜率存在时,设切线方程的斜率为k,则切线方程为y-6=k(x+1),即kx-y+6+k=0,
由圆心(-3,2)到切线的距离d=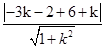 =2,
=2,
化简得(2k-4)2=4(1+k2),解得k=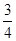 ,所以,切线方程为y-6=
,所以,切线方程为y-6=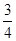 (x+1),即3x-4y+27=0.
(x+1),即3x-4y+27=0.
综上知,切线方程为:3x-4y+27=0或x=-1.
考点:直线与圆的位置关系,点到直线的距离公式。
点评:中档题,利用数形结合思想,分析切线方程有两条,故考虑切线的斜率存在与不存在的两种情况,本题易错---漏解。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
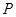 是圆
是圆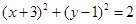 上的动点,
上的动点,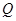 是直线
是直线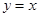 上的动点,则
上的动点,则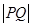 的最小值为 ________________
的最小值为 ________________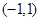 的直线与圆
的直线与圆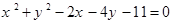 截得的弦长为
截得的弦长为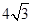 ,则该直线的方程为 .
,则该直线的方程为 . 与直线
与直线 及
及 都相切,且圆心在直线
都相切,且圆心在直线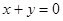 上,则圆
上,则圆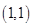 在圆
在圆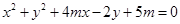 外,则实数
外,则实数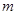 的取值范围是 。
的取值范围是 。 (
(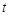 为参数)与圆
为参数)与圆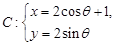 (
(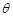 为参数),则直线
为参数),则直线 的倾斜角及圆心
的倾斜角及圆心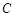 的直角坐标分别是
的直角坐标分别是 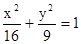 上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .