题目内容
在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，底面ABCD为菱形，∠BAD=60°，P为AB的中点，Q为CD1的中点．（1）求证：DP⊥平面A1ABB1；
（2）求证：PQ∥平面ADD1A1．
分析：（1）利用菱形和等边三角形的性质、线面垂直的判定定理即可证明；
（2）利用三角形的中位线定理、平行四边形的性质、线面、面面平行的判定与性质定理即可证明．
（2）利用三角形的中位线定理、平行四边形的性质、线面、面面平行的判定与性质定理即可证明．
解答：证明：（1）连接DB，由菱形ABCD可得AB=AD，又∠DAB=60°，∴△ABD是等边三角形，
∵P为AB的中点，∴DP⊥AB．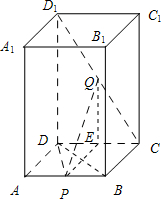
∵AA1⊥平面ABCD，∴AA1⊥DP．
又AA1∩AB=A，∴DP⊥平面A1ABB1．
（2）取CD的中点E，连接PE，EQ，又Q为CD1的中点，根据三角形的中位线定理可得EQ∥DD1，
∵EQ?平面ADD1A1．DD1?平面ADD1A1．
∴EQ∥平面ADD1A1．
由于平行四边形APED可得EP∥AD，同理可得EP∥平面ADD1A1．
∵EP∩EQ=E，∴平面EPQ∥平面ADD1A1．∴PQ∥平面ADD1A1．
∵P为AB的中点，∴DP⊥AB．
∵AA1⊥平面ABCD，∴AA1⊥DP．
又AA1∩AB=A，∴DP⊥平面A1ABB1．
（2）取CD的中点E，连接PE，EQ，又Q为CD1的中点，根据三角形的中位线定理可得EQ∥DD1，
∵EQ?平面ADD1A1．DD1?平面ADD1A1．
∴EQ∥平面ADD1A1．
由于平行四边形APED可得EP∥AD，同理可得EP∥平面ADD1A1．
∵EP∩EQ=E，∴平面EPQ∥平面ADD1A1．∴PQ∥平面ADD1A1．
点评：熟练掌握菱形和等边三角形的性质、线面垂直的判定定理、三角形的中位线定理、平行四边形的性质、线面、面面平行的判定与性质定理是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中，AB=1，AA′=
，则A、C两点间的球面距离为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，侧棱与底面垂直，E，F分别是AB1，BC1的中点，则以下结论中不成立的是（ ）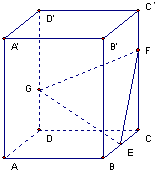
如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：
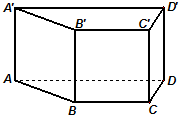在高为1的直四棱柱ABCD-A'B'C'D'中，底面ABCD是等腰梯形，AB=BC=CD=1，AD=2．