题目内容
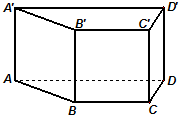 在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.
在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2. (1)求异面直线BC'与CD'所成的角;
(2)求被截面ACD'所截的两部分几何体的体积比.
分析:(1)设AD的中点为E,A'D'的中点为E',连接BE'.由题意证出BCDE-B'C'D'E'是底面为菱形的直四棱柱,可得
∠E'BC'是异面直线BC'与CD'所成的角.在△BC'E'中,利用余弦定理加以计算,即可得到异面直线BC'与CD'所成的角是arccos
.
(2)由锥体的体积公式,算出三棱锥D'-ACD的体积,再用四棱柱ABCD-A'B'C'D'的体积减去三棱锥D'-ACD的体积,将三棱锥D'-ACD的体积与作减法所得到的体积求比值,即可得到所求体积比.
∠E'BC'是异面直线BC'与CD'所成的角.在△BC'E'中,利用余弦定理加以计算,即可得到异面直线BC'与CD'所成的角是arccos
| 3 |
| 4 |
(2)由锥体的体积公式,算出三棱锥D'-ACD的体积,再用四棱柱ABCD-A'B'C'D'的体积减去三棱锥D'-ACD的体积,将三棱锥D'-ACD的体积与作减法所得到的体积求比值,即可得到所求体积比.
解答:解:(1)由已知ABCD和A'B'C'D'是全等的底角为60°的等腰梯形,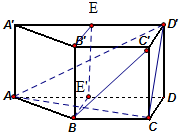
B'BCC'和C'CDD'是边长为1的正方形.
设AD的中点为E,A'D'的中点为E',连接BE'.
∵BCDE-B'C'D'E'是底面为菱形的直四棱柱,
∴BE'∥CD',∠E'BC'是异面直线BC'与CD'所成的角.
∵在△BC'E'中,BC′=BE′=
, C′E′=1,cos ∠ E′BC′=
=
,
∴异面直线BC'与CD'所成的角是arccos
.
(2)求被截面ACD'所截的两部分几何体的体积比.
∵VD'-ACD=
×
×
×1×1=
,VABCD-A'B'C'D'=
×
×1=
,
VABCD-A'B'C'D'-VD'-ACD=
-
=
,
∴被截面ACD'所截的两部分几何体的体积比是
:
=2:7.

B'BCC'和C'CDD'是边长为1的正方形.
设AD的中点为E,A'D'的中点为E',连接BE'.
∵BCDE-B'C'D'E'是底面为菱形的直四棱柱,
∴BE'∥CD',∠E'BC'是异面直线BC'与CD'所成的角.
∵在△BC'E'中,BC′=BE′=
| 2 |
| 2+2-1 | ||||
2×
|
| 3 |
| 4 |
∴异面直线BC'与CD'所成的角是arccos
| 3 |
| 4 |
(2)求被截面ACD'所截的两部分几何体的体积比.
∵VD'-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |
| 1+2 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
VABCD-A'B'C'D'-VD'-ACD=
3
| ||
| 4 |
| ||
| 6 |
7
| ||
| 12 |
∴被截面ACD'所截的两部分几何体的体积比是
| ||
| 6 |
7
| ||
| 12 |
点评:本题在特殊的四棱柱中求异面直线所成角,并求被截面分成的两部分的体积之比.着重考查了异面直线所成角的定义与求法和柱体、锥体体积求法等知识,属于中档题.

练习册系列答案
相关题目
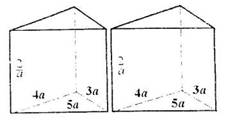 有两个相同的直三棱柱,高为
有两个相同的直三棱柱,高为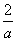 ,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是
.
,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是
.