题目内容
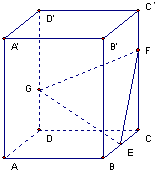 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:(Ⅰ)C′到面EFG的距离;
(Ⅱ)DA与面EFG所成的角的正弦值;
(III)在直线BB'上是否存在点P,使得DP∥面EFG?,若存在,找出点P的位置,若不存在,试说明理由.
分析:(I)以D为原点建立空间直角坐标系,并求出面EFG的一个法向量
,及面EFG上任一点与C′连线的方向向量,代入公式d=
中,即得到C′到面EFG的距离;
(Ⅱ)求出DA的方向向量,结合(I)中所求的面EFG的法向量
的坐标,代入向量夹角公式,即可得到DA与面EFG所成的角的正弦值;
(III)设出P点坐标,求出DP的方向向量,根据DP∥面EFG,则
•
=0,可以构造关于P点坐标的方程组,解方程组,即可得P点坐标.
| n |
|
| ||||
|
|
(Ⅱ)求出DA的方向向量,结合(I)中所求的面EFG的法向量
| n |
(III)设出P点坐标,求出DP的方向向量,根据DP∥面EFG,则
| DP |
| n |
解答: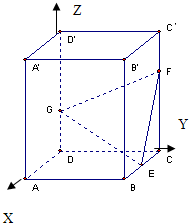 解:如图,以D为原点建立空间直角坐标系
解:如图,以D为原点建立空间直角坐标系
则E(1,2,0),F(0,2,2),G(0,0,1)
∴
=(-1,0,2),
=(0,-2,-1),
设
=(x,y,z)为面EFG的法向量,则
•
=0,
•
=0,
⇒x=2z,z=-2y,取y=1,
得
=(-4,1,-2)…(4分)
(Ⅰ)∵
=(0,0,-1),
∴C’到面EFG的距离为d=
=
=
…(6分)
(Ⅱ)
=(2,0,0),设DA与面EFG所成的角为θ,
则sinθ=
=
. …(10分)
( III)存在点P,在B点下方且BP=3,此时P(2,2,-3)
=(2,2,-3),∴
•
=0,∴DP∥面EFG.…(14分)
 解:如图,以D为原点建立空间直角坐标系
解:如图,以D为原点建立空间直角坐标系则E(1,2,0),F(0,2,2),G(0,0,1)
∴
| EF |
| FG |
设
| n |
| EF |
| n |
| FG |
| n |
⇒x=2z,z=-2y,取y=1,
得
| n |
(Ⅰ)∵
| C′F |
∴C’到面EFG的距离为d=
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 21 |
(Ⅱ)
| DA |
则sinθ=
|
| ||||
|
|
4
| ||
| 21 |
( III)存在点P,在B点下方且BP=3,此时P(2,2,-3)
| DP |
| DP |
| n |
点评:本题考查的知识点是用空间向量求直线与平面的夹角,直线与平面平行的判定,点到平面的距离计算,其中由于三个小题的结论均与面EFG有关,故求出平面EFG的法向量是解答本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
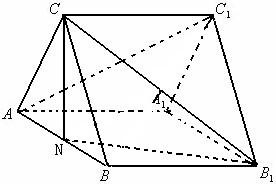 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
