题目内容
16.已知向量($\overrightarrow{a}$+3$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-5$\overrightarrow{b}$)且($\overrightarrow{a}$-4$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-2$\overrightarrow{b}$),求向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角θ.分析 向量($\overrightarrow{a}$+3$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-5$\overrightarrow{b}$)且($\overrightarrow{a}$-4$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-2$\overrightarrow{b}$),可得$7{\overrightarrow{a}}^{2}+16\overrightarrow{a}•\overrightarrow{b}-15{\overrightarrow{b}}^{2}$=0,$7{\overrightarrow{a}}^{2}-30\overrightarrow{a}•\overrightarrow{b}$+8${\overrightarrow{b}}^{2}$=0,化为$|\overrightarrow{b}|=2|\overrightarrow{a}|cosθ$,代入$7{\overrightarrow{a}}^{2}+16\overrightarrow{a}•\overrightarrow{b}-15{\overrightarrow{b}}^{2}$=0,解出即可.
解答 解:∵向量($\overrightarrow{a}$+3$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-5$\overrightarrow{b}$)且($\overrightarrow{a}$-4$\overrightarrow{b}$)⊥(7$\overrightarrow{a}$-2$\overrightarrow{b}$),
∴$7{\overrightarrow{a}}^{2}+16\overrightarrow{a}•\overrightarrow{b}-15{\overrightarrow{b}}^{2}$=0,
$7{\overrightarrow{a}}^{2}-30\overrightarrow{a}•\overrightarrow{b}$+8${\overrightarrow{b}}^{2}$=0,
∴$2|\overrightarrow{a}||\overrightarrow{b}|cosθ$=$|\overrightarrow{b}{|}^{2}$,
化为$|\overrightarrow{b}|=2|\overrightarrow{a}|cosθ$,代入$7{\overrightarrow{a}}^{2}+16\overrightarrow{a}•\overrightarrow{b}-15{\overrightarrow{b}}^{2}$=0,
化为:$7|\overrightarrow{a}{|}^{2}$+16$|\overrightarrow{a}|×2|\overrightarrow{a}|co{s}^{2}θ$-$15×4|\overrightarrow{a}{|}^{2}$cos2θ,
∴$cosθ=±\frac{1}{2}$,
∴θ=$\frac{π}{3}$或$\frac{2π}{3}$.
点评 本题考查了数量积的定义及其运算性质,考查了推理能力与计算能力,属于中档题.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案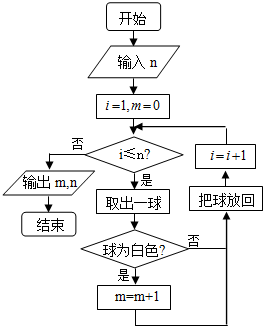
①请估计:当n很大时,摸到白球的频率将会接近0.60.
②假如你去摸一次球,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
③口袋中白球的个数约为12,黑球的个数约为8.
表1:
| n | 100 | 150 | 200 | 500 | 800 | 1000 |
| m | 58 | 96 | 116 | 295 | 484 | 601 |
| A. | y=-4x+3 | B. | y=-4x-3 | C. | y=4x+3 | D. | y=4x-3 |
