题目内容
设二次函数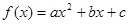 ,方程
,方程 有两个相等的实根,且
有两个相等的实根,且 .
.
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)求 的图象与两坐标轴所围成图形的面积.
的图象与两坐标轴所围成图形的面积.
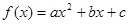 ,方程
,方程 有两个相等的实根,且
有两个相等的实根,且 .
.(Ⅰ)求
 的表达式;
的表达式;(Ⅱ)求
 的图象与两坐标轴所围成图形的面积.
的图象与两坐标轴所围成图形的面积.:(1)f′(x)=2ax+b.
又f′(x)=2x+2,所以a=1,b=2.
又方程f(x)=0有两个相等实根,
即x2+2x+c=0有两个相等实根,
所以Δ=4-4c=0,即c=1.
故f(x)=x2+2x+1.--------------------------------------------------------------------5分
(2)依题意,所求面积为S=(x2+2x+1)dx,
取F(x)=x3+x2+x,则F′(x)=x2+2x+1,
∴S=(x2+2x+1)dx=F(0)-F(-1)=.--------------------------------------10分
又f′(x)=2x+2,所以a=1,b=2.
又方程f(x)=0有两个相等实根,
即x2+2x+c=0有两个相等实根,
所以Δ=4-4c=0,即c=1.
故f(x)=x2+2x+1.--------------------------------------------------------------------5分
(2)依题意,所求面积为S=(x2+2x+1)dx,
取F(x)=x3+x2+x,则F′(x)=x2+2x+1,
∴S=(x2+2x+1)dx=F(0)-F(-1)=.--------------------------------------10分
略

练习册系列答案
相关题目
 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图象关于
的图象关于 对称.若对任意的
对称.若对任意的 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的取值范围是 .
的取值范围是 . 的图象经过点
的图象经过点 .
. 的值;
的值;  在
在 点处的切线方程.
点处的切线方程.
 ,猜想
,猜想 的表达式为
的表达式为 ;
; ;
; ;
; .
. 为
为 的各位数字之和,如
的各位数字之和,如 ,则
,则 记
记 则
则 =
= 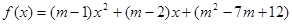 为偶函数,则
为偶函数,则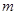 的值
的值


 满足
满足 时,
时, ,若
,若 ,则
,则 = 。
= 。 的定义域为R,求实数m的取值范围
的定义域为R,求实数m的取值范围 ,则
,则 的值为( )
的值为( )

